参考书目：Digital Processing of Synthetic Aperture Radar Data Algorithms and Implementation

本部分内容作为本人本科毕业设计和研究生阶段的前置学习内容，方便以后查阅。

第一部分 合成孔径雷达基础

第一章 概论

SAR的不同工作模式

信噪比（Signal-to-Noise，SNR）

SAR系统的一个重要参数是图像信噪比。SAR信号的信噪比可以由雷达方程导出。雷达方程表明，雷达接收功率是发射功率、雷达与目标之间的距离，以及许多雷达系统和散射体变量的函数。为建立图像质量与雷达发射功率之间的定量关系，一般将雷达方程表示成图像信噪比的形式，若图像包含分布目标（一般指杂波），则信噪比为

其中P_{ave}为平均发射功率，G为天线增益，\lambda为雷达波长，\sigma_0为地面目标的归一化后向散射系数，c为光速，R为雷达与反射体的距离，K为玻尔兹曼常数，T为接收机温度，B_T为发射信号带宽，F_n为接收机噪声系数，L_s为系统损失，V为平台速度，\theta_i为波束入射角。

距离徒动（Range Cell Migration,RCM）

由于在合成孔径内传感器的移动，雷达与目标的距离随时间变化，这个变化所引起的回波数据的多普勒频移构成了合成孔径处理的基础。然而，这种距离变化同时也导致了距离徒动现象^1，使数据处理变得更加复杂了。

1 即同一目标在不同脉冲发射周期内，回波信号被接收之后，数据记录位置发生变化的现象。

距离徒动校正（Range Cell Migration Correction,RCMC）

要点：不过度增加处理复杂度的同时精确地校正RCM。

雷达接收到回波以后，就对数据进行采样和存储。数据处理是一个二维过程，但一般分成距离向和方位向两个互相独立的一维处理过程。当回波能量在一个合成孔径时间内沿距离向没有明显的变化时，这种分离是非常简单的。这里的“明显”依赖于距离向的采样密度。如果回波能量分布沿距离向的变化（或称距离徙动）超过了一个距离向采样点（或称距离单元），就认为这种变化是“明显”的，在成像处理时必须加以考虑。

第二章 信号处理基础

2.2 线性卷积

2.2.1 连续时间卷积

在连续时域内，卷积可写为(y = s*h)(t)=\int_{-\infty}^{+\infty} s(u)\,h(t-u)\,du =\int_{-\infty}^{+\infty} s(t-u)\,h(u)\,du .

MATLAB手写“时域”线性卷积（不依赖 conv）

function y = lconv_time(x, h)
%   LCONV_TIME  时域线性卷积（不调用内置 conv）
%   y = lconv_time(x, h)
%   输出 y 的长度为 length(x)+length(h)-1
%
%   说明：默认输出列向量；若两输入均为行向量则输出行向量

    x_is_row = isrow(x);
    h_is_row = isrow(h);

    x = x(:);    % 列向量
    h = h(:);    % 列向量
    Nx = length(x);
    Nh = length(h);
    Ny = Nx + Nh - 1;
    y  = zeros(Ny, 1);

    % 双循环：y[n] = sum_{k} x[k] * h[n-k+1]
    for n = 1:Ny
        kmin = max(1, n - Nh + 1);
        kmax = min(n, Nx);
        % 等价于： for k = 1:Nx, 若 1<=n-k+1<=Nh 再累加
        for k = kmin:kmax
            y(n) = y(n) + x(k) * h(n - k + 1);
        end
    end

    % 若两输入均为行向量，则转为行向量输出
    if x_is_row && h_is_row
        y = y.';
    end
end

% ------------ 示例 -------------
% x = [1 2 3]; h = [1 1 1];
% y = lconv_time(x, h)   % -> [1 3 6 5 3]

相关

相关的定义为{\;(s*h)(t)=\int_{-\infty}^{\infty} s(u)\,h(t-u)\,du\;}

与卷积不同：滤波器的时间轴无需进行反转；若滤波器是复的，则还需取共轭。

2.3 傅立叶变换

2.3.1 连续时间傅立叶变换

傅立叶变换的优势：函数g(t)可以表示为一组幅度和相位各不相同的正弦信号的和。

连续时间傅立叶变换：X(f)=\int_{-\infty}^{\infty} x(t)\,e^{-j2\pi f t}\,dt,\qquad x(t)=\int_{-\infty}^{\infty} X(f)\,e^{j2\pi f t}\,df .

%% ctft_demo.m
% 数值连续时间傅里叶变换（CTFT，角频率域）演示
% X(ω) = ∫ x(t) e^{-j ω t} dt,  x(t) = (1/2π) ∫ X(ω) e^{j ω t} dω
clear; close all; clc;

%% 全局数值网格设置（可根据信号时间/频率特性调整）
Twin = 10;            % 时间窗总时长（秒），[-Twin/2, Twin/2]
dt   = 1e-3;          % 采样间隔（秒）
t    = (-Twin/2:dt:Twin/2).';    % 列向量

wmax = 200;           % 频域范围（rad/s）
Nw   = 4001;          % 频域采样点数（奇数便于对称）
w    = linspace(-wmax, wmax, Nw).';   % 列向量

%% 工具函数（见文末）：ctft_numeric, ictft, plot_spec, rectfun

%% 示例 1：矩形脉冲  x(t) = rect(t/T0)  (宽度 T0)
T0 = 1.0;
x1 = rectfun(t/T0);                      % rect(t/T0), 中心对齐
[X1w] = ctft_numeric(x1, t, w);          % 数值 CTFT
X1w_ana = T0 * sinc((w*T0)/2);           % 解析解（sinc(x)=sin(x)/x, x=ωT0/2）

figure('Name','Example 1: Rect pulse');
plot_spec(w, X1w, 'Rect pulse: numeric CTFT');
hold on; plot(w, abs(X1w_ana), 'LineWidth', 1.0, 'LineStyle', '--'); legend('|\bfX_{num}|','|\bfX_{ana}|');

% 重构检查
x1_rec = ictft(w, X1w, t);
err1 = norm(x1 - x1_rec, 2) / norm(x1, 2);
fprintf('Example 1 recon RMSE ratio: %.3e\n', err1);

% Parseval 检查：∫|x(t)|^2 dt  ≈ (1/2π)∫|X(ω)|^2 dω
E_time = trapz(t, abs(x1).^2);
E_freq = (1/(2*pi)) * trapz(w, abs(X1w).^2);
fprintf('Example 1 Parseval: time=%.6f, freq=%.6f, rel.err=%.3e\n', E_time, E_freq, abs(E_time-E_freq)/E_time);

%% ---------------------- 本文件尾部的工具函数 ----------------------
function [Xw] = ctft_numeric(x, t, w)
% 数值 CTFT:  X(ω) ≈ ∫ x(t) e^{-jωt} dt  （trapz 实现）
% 输入: x(Nt×1), t(Nt×1), w(Nw×1); 输出: Xw(Nw×1)
    x  = x(:);  t = t(:);  w = w(:);
    % 生成 Nt×Nw 的指数矩阵，并沿 t 维做数值积分
    E  = exp(-1j * (t * w.'));       % Nt x Nw
    integrand = x .* E;              % 隐式广播：每列乘以 x
    Xrow = trapz(t, integrand, 1);   % 1×Nw
    Xw  = Xrow.';                    % Nw×1
end

function x = ictft(w, Xw, t)
% 数值反变换: x(t) ≈ (1/2π) ∫ X(ω) e^{jωt} dω
% 输入: w(Nw×1), Xw(Nw×1), t(Nt×1); 输出: x(Nt×1)
    t = t(:); w = w(:); Xw = Xw(:);
    E  = exp( 1j * (t * w.'));       % Nt x Nw
    integrand = (ones(numel(t),1) * Xw.') .* E;    % Nt x Nw
    x = (1/(2*pi)) * trapz(w, integrand, 2);       % Nt×1
end

function plot_spec(w, Xw, ttl)
% 绘制幅度与相位（相位用 unwrap）
    if size(w,2)>1, w = w(:); end
    if size(Xw,2)>1, Xw = Xw(:); end
    tiledlayout(2,1);
    nexttile; plot(w, abs(Xw), 'LineWidth', 1.2); grid on;
    xlabel('\omega (rad/s)'); ylabel('|X(\omega)|'); title(ttl);
    nexttile; plot(w, unwrap(angle(Xw)), 'LineWidth', 1.0); grid on;
    xlabel('\omega (rad/s)'); ylabel('\angle X(\omega) (rad)');
end

function y = rectfun(x)
% rect(x)：|x|<=1/2 为 1，其他为 0；边界取 1
    y = double(abs(x) <= 0.5);
end

Example 1 recon RMSE ratio: 5.618e-02

Example 1 Parseval: time=1.001000, freq=0.997840, rel.err=3.157e-03

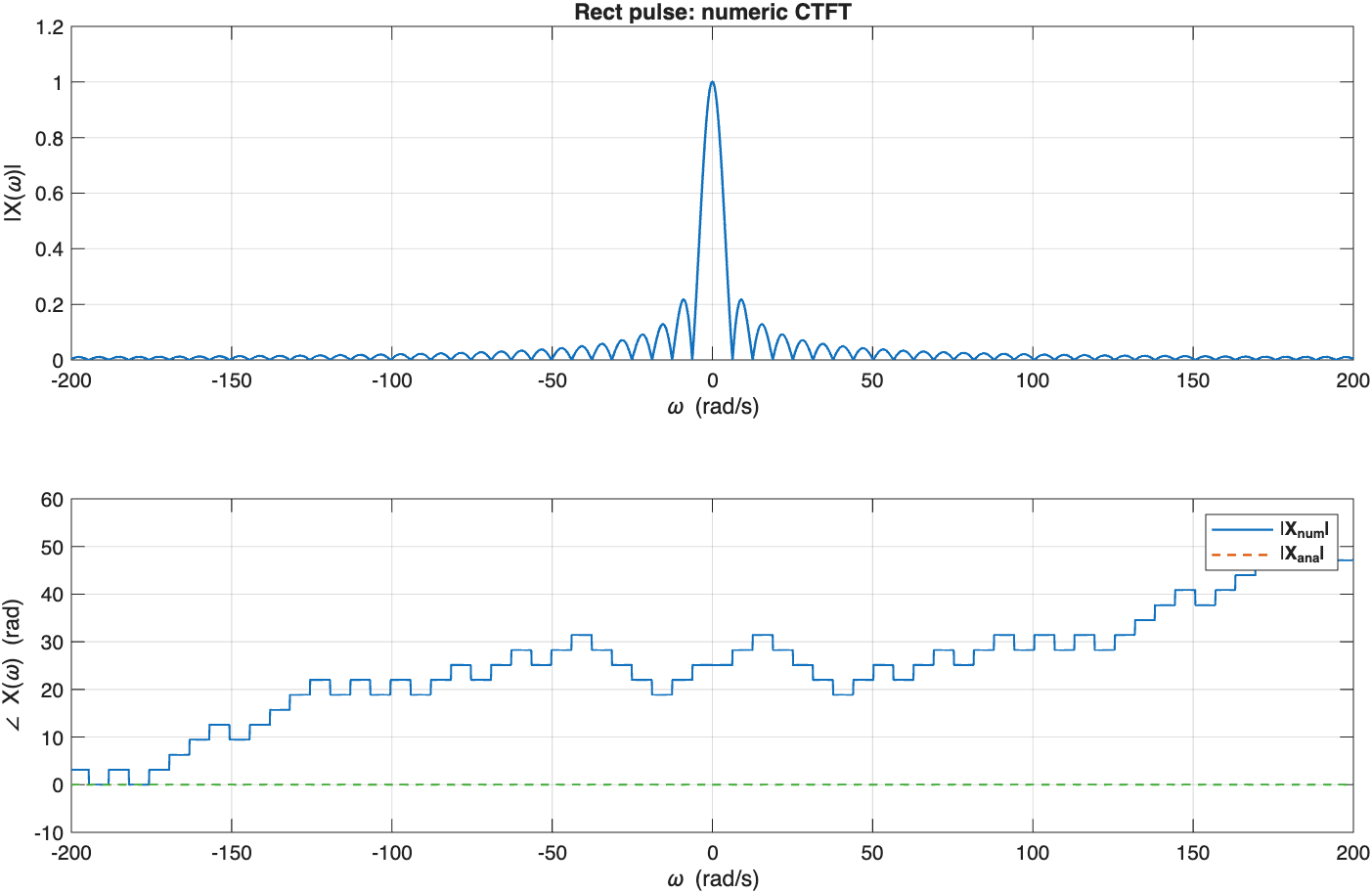
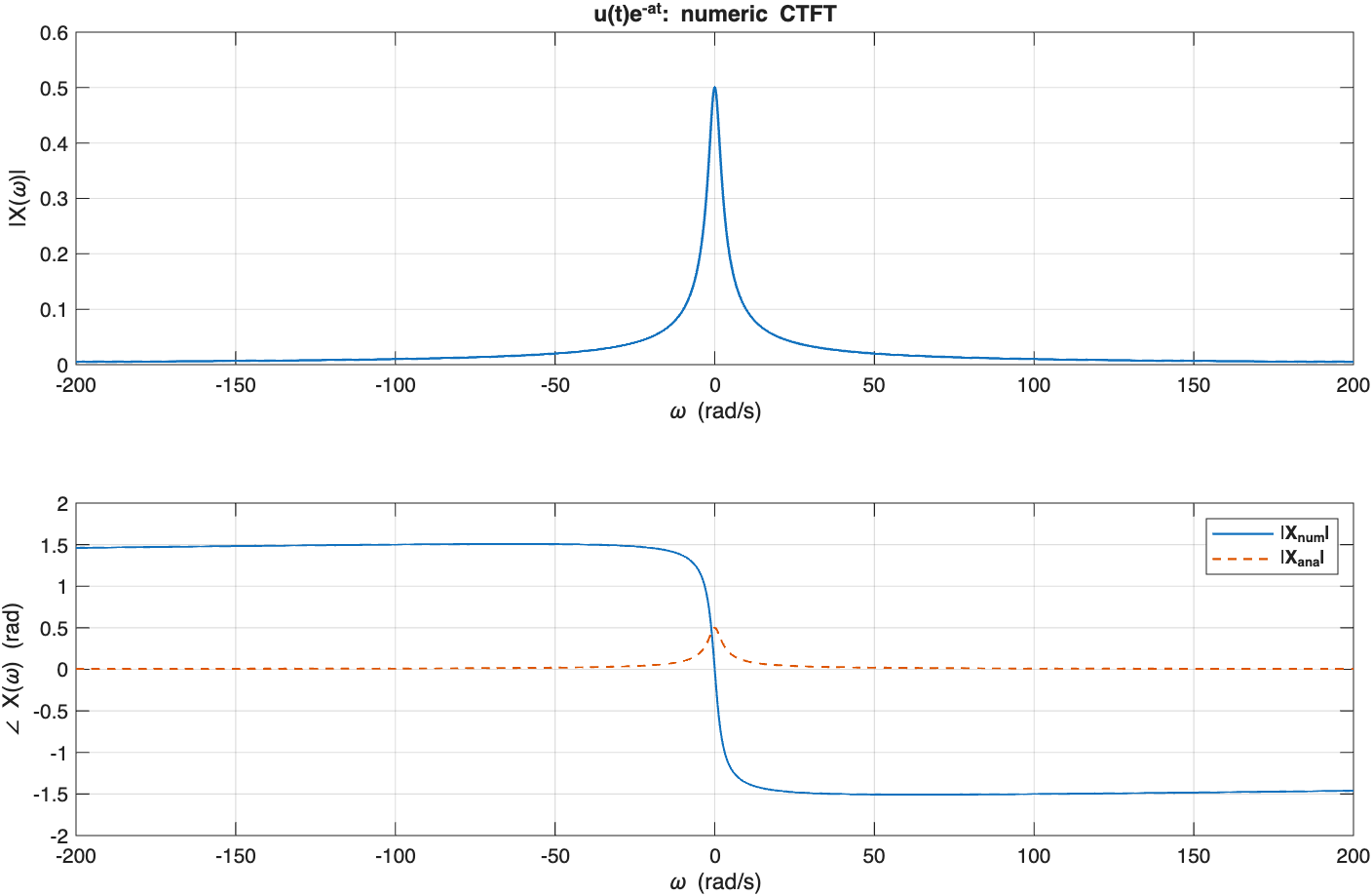
%% 示例 2：单边指数  x(t)=u(t) e^{-a t}, a>0
a = 2;
x2 = (t>=0).*exp(-a*t);
[X2w] = ctft_numeric(x2, t, w);
X2w_ana = 1./(a + 1j*w);

figure('Name','Example 2: One-sided exponential');
plot_spec(w, X2w, 'u(t)e^{-at}: numeric CTFT');
hold on; plot(w, abs(X2w_ana), 'LineWidth', 1.0, 'LineStyle', '--'); legend('|\bfX_{num}|','|\bfX_{ana}|');

x2_rec = ictft(w, X2w, t);
err2 = norm(x2 - x2_rec, 2) / norm(x2, 2);
fprintf('Example 2 recon RMSE ratio: %.3e\n', err2);

E_time = trapz(t, abs(x2).^2);
E_freq = (1/(2*pi)) * trapz(w, abs(X2w).^2);
fprintf('Example 2 Parseval: time=%.6f, freq=%.6f, rel.err=%.3e\n', E_time, E_freq, abs(E_time-E_freq)/E_time);

Example 2 recon RMSE ratio: 7.964e-02

Example 2 Parseval: time=0.250500, freq=0.248911, rel.err=6.345e-03

%% 示例 3：Gaussian  x(t)=exp(-a t^2), a>0
ag = 1.5;
x3 = exp(-ag*t.^2);
[X3w] = ctft_numeric(x3, t, w);
X3w_ana = sqrt(pi/ag) * exp(-(w.^2)/(4*ag));

figure('Name','Example 3: Gaussian');
plot_spec(w, X3w, 'exp(-a t^2): numeric CTFT');
hold on; plot(w, abs(X3w_ana), 'LineWidth', 1.0, 'LineStyle', '--'); legend('|\bfX_{num}|','|\bfX_{ana}|');

x3_rec = ictft(w, X3w, t);
err3 = norm(x3 - x3_rec, 2) / norm(x3, 2);
fprintf('Example 3 recon RMSE ratio: %.3e\n', err3);

E_time = trapz(t, abs(x3).^2);
E_freq = (1/(2*pi)) * trapz(w, abs(X3w).^2);
fprintf('Example 3 Parseval: time=%.6f, freq=%.6f, rel.err=%.3e\n', E_time, E_freq, abs(E_time-E_freq)/E_time);

Example 3 recon RMSE ratio: 3.037e-16

Example 3 Parseval: time=1.023327, freq=1.023327, rel.err=2.170e-16

%% 进阶：近似“余弦→谱线”（有限窗导致谱泄漏）
f0 = 5;                        % Hz（为了演示，便于观察）
w0 = 2*pi*f0;                  % rad/s
x4 = cos(w0*t) .* rectfun(t/4);% 给定4秒窗，近似观测
[X4w] = ctft_numeric(x4, t, w);

figure('Name','Example 4: Windowed cosine');
plot_spec(w, X4w, 'cos(ω0 t) with 4s window');
% 理论理想是 π[δ(ω-ω0)+δ(ω+ω0)]；有限窗→近似sinc 主瓣+旁瓣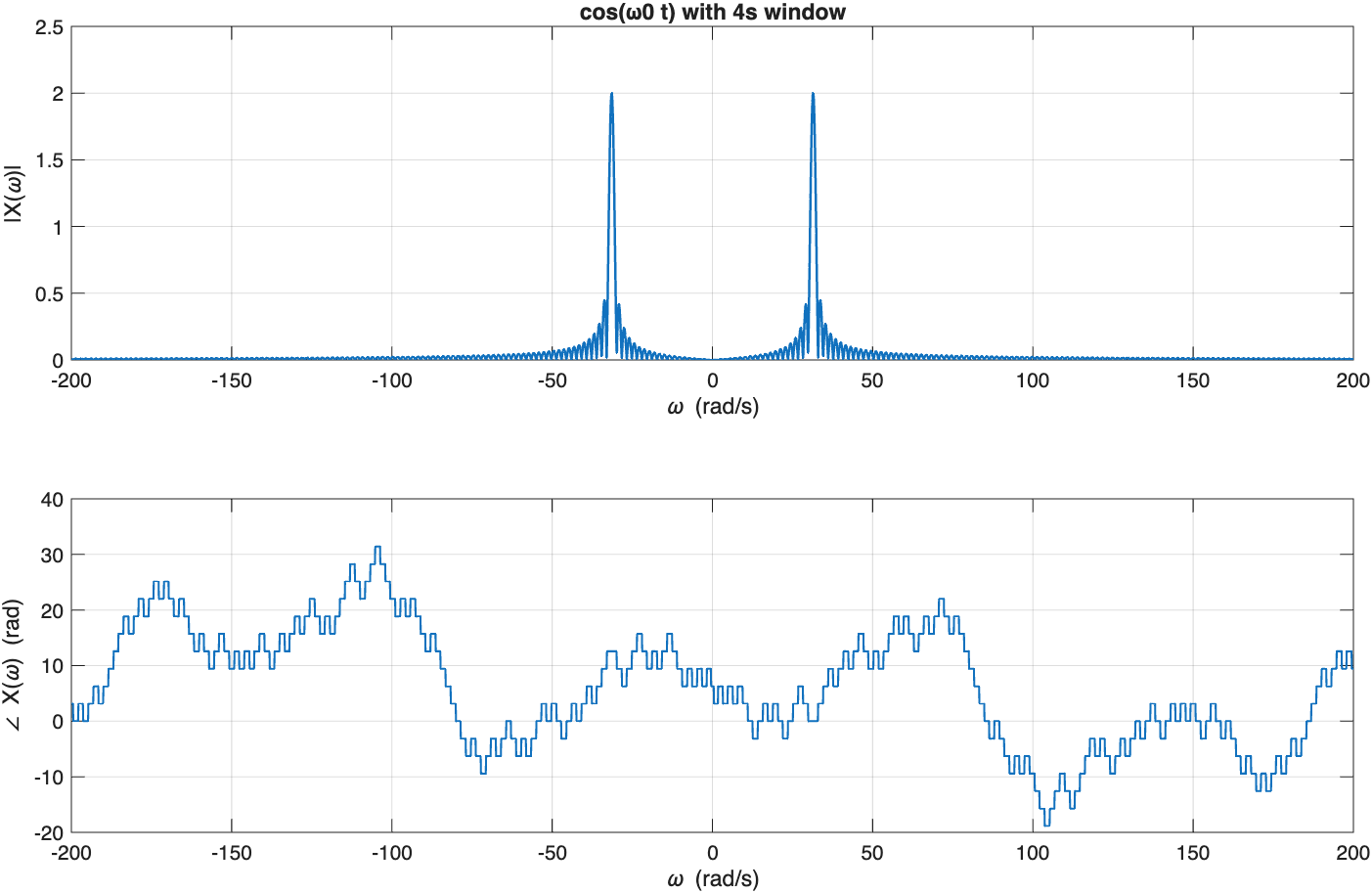

2.3.2 离散傅立叶变换

2.3.3 傅立叶变换的性质

推导部分参考教材：

[6] A. Papoulis. The Fourier Integral and Its Applications. McGraw-Hill College Division, New York, 1962.

[7] E. O. Brigham. The Fast Fourier Transform: An Introduction to Its Theory and Application. Prentice Hall, Upper Saddle River, NJ, 1974.

[8] R. N. Bracewell. The Fourier Transform and Its Applications. WCB/McGraw-Hill, New York, 3rd edition, 1999.

（1）复共轭

含义： 实信号的谱具厄米对称F(-\omega)=F^*(\omega)。常用于验证回波与脉压结果的谱对称性与相位一致性。

推导：\mathcal{F}\{f^\}(\omega)=\int f^(t)e^{-j\omega t}dt =\left[\int f(t)e^{+j\omega t}dt\right]^* =\left[F(-\omega)\right]^=F^(-\omega).

（2）线性

含义：配滤波、孔径合成等可分步线性处理叠加。

推导： 由积分的线性性直接成立。

（3）尺度变换特性

含义： 频域轴伸缩/重采样（如 Stolt 映射的本质）与时域尺度变化互为倒数关系。

1D：\mathcal{F}\{f(a t)\}(\omega)=\frac{1}{|a|}\,F\!\left(\frac{\omega}{a}\right)

2D 一般线性变换：若g(\boldsymbol{x})=f(\mathbf{A}\boldsymbol{x})（\mathbf{A} 可为缩放、剪切、旋转…），则G(\boldsymbol{\omega})=\frac{1}{|\det\mathbf{A}|}\,F\!\left(\mathbf{A}^{-T}\boldsymbol{\omega}\right)

推导：令u=at\Rightarrow dt=du/a：\int f(at) e^{-j\omega t}dt =\frac{1}{|a|}\int f(u) e^{-j(\omega/a) u}\,du

（4）位移/调制

时间位移：\mathcal{F}\{f(t-t_0)\}=e^{-j\omega t_0}F(\omega).

调制：\mathcal{F}\{f(t)e^{j\omega_0 t}\}=F(\omega-\omega_0).

含义： 距离/方位向平移\Rightarrow频域线性相位；速度引起多普勒中心漂移\Rightarrow频谱搬移。

（5）均值

（6）对称性

（7）Parseval定理

1D：\int_{-\infty}^{\infty} |f(t)|^2 dt=\frac{1}{2\pi}\int_{-\infty}^{\infty} |F(\omega)|^2 d\omega .

含义： 能量/信噪比在时频域保持一致；用于定标与滤波器能量约束。

（8）卷积/乘法

含义： 匹配滤波（脉压/方位压缩）常在频域用“点乘”实现；时域乘窗 \Rightarrow 频域与 sinc 类核卷积（谱泄漏/旁瓣）。

（9）补零

核心： 对长度 N 的序列x[n] 在末尾补零到 L>N 并做 L 点 DFT：X_L[k]=\sum_{n=0}^{L-1}x_{\text{zp}}[n]e^{-j2\pi kn/L} =\sum_{n=0}^{N-1}x[n]e^{-j2\pi kn/L}=X\!\left(e^{j\omega}\right)\big|_{\omega=2\pi k/L}.

这等价于在频域更密集采样 DTFT（插值光滑），并不增加新信息。

含义： 细化距离/方位向像素间隔（视觉上更平滑、便于峰值定位），但不提升真正分辨率；配合峰值插值用于亚像素估计、RVP 补偿等。

（10）二维扭曲和旋转

含义： Keystone 变换、距离-多普勒耦合校正、本振漂移校正等常本质上是 2D 线性变换（剪切/缩放/旋转）在某个域（时-频或频-频）内的实现。

2.3.4 傅立叶变换示例

%% demo_rect_sinc_FT.m
% 演示：rect(t/T) <-> T*sinc(f*T)；sinc(t/T) <-> T*rect(f*T)
% 采用 Fourier 变换定义：X(f) = ∫ x(t) e^{-j2π f t} dt  ，频率单位 Hz
% 说明：
% 1) 数值CTFT用：X_fft ≈ Δt * FFT{x(t)} 并做fftshift，频率栅格 f = (-N/2:N/2-1)/(N*Δt)
% 2) MATLAB中使用"归一化 sinc"定义：sinc(u) = sin(pi*u)/(pi*u)

clear; close all; clc;

%% 公用参数（时间窗、采样与频率轴）
Trect = 1;            % 矩形脉宽（秒）——可自行修改
L = 16*Trect;         % 总观察时长（越长，频域越细 & 截断效应越小）
N = 2^15;             % 采样点数（越大，频率分辨率越高）
dt = L/N;             % 采样间隔
t = (-N/2:N/2-1).' * dt;      % 对称时间轴，列向量
[f,~] = make_freq_axis(N, dt); % 频率轴（Hz）

% 自定义函数句柄（避免工具箱依赖）
sincn = @(u) sin(pi*u)./(pi*u); % 归一化sinc，u=0处稍后单独处理
rectp = @(x,Tw) double(abs(x) < Tw/2) + 0.5*double(abs(x) == Tw/2); % 矩形脉冲

%% --------------------- 示例 1：矩形 -> sinc ---------------------
x1 = rectp(t, Trect);                        % x1(t) = rect(t/Trect)
X1_num = ctft_fft(x1, dt);                   % 数值CTFT近似
X1_ana = Trect * safe_sinc(f*Trect, sincn);  % 解析：T * sinc(f*T)

figure('Name','Rect <-> Sinc','Color','w');
tiledlayout(2,2,"Padding","compact","TileSpacing","compact");

% 时域
nexttile; plot(t, x1, 'LineWidth', 1); grid on;
xlabel('t (s)'); ylabel('x_1(t)'); title('Rect：x_1(t)=rect(t/T)');
xlim([-1.5*Trect, 1.5*Trect]);

% 频域幅度
nexttile; plot(f, abs(X1_num), 'LineWidth', 1); hold on;
plot(f, abs(X1_ana), '--', 'LineWidth', 1);
grid on; xlabel('f (Hz)'); ylabel('|X_1(f)|');
title('FT 幅度：数值 vs 解析'); legend('Numerical (FFT)','Analytic','Location','best');
xlim([-10/Trect, 10/Trect]);

% 频域相位（只在幅度较大处显示更有意义）
mask = abs(X1_ana) > 1e-2*max(abs(X1_ana));
nexttile; plot(f(mask), angle(X1_num(mask)), '.', 'MarkerSize', 6); grid on;
xlabel('f (Hz)'); ylabel('∠X_1(f) (rad)'); title('FT 相位（数值）');

% 误差
nexttile; plot(f, abs(X1_num - X1_ana), 'LineWidth', 1); grid on;
xlabel('f (Hz)'); ylabel('|X_{num}-X_{ana}|'); title('数值-解析 误差');
xlim([-10/Trect, 10/Trect]);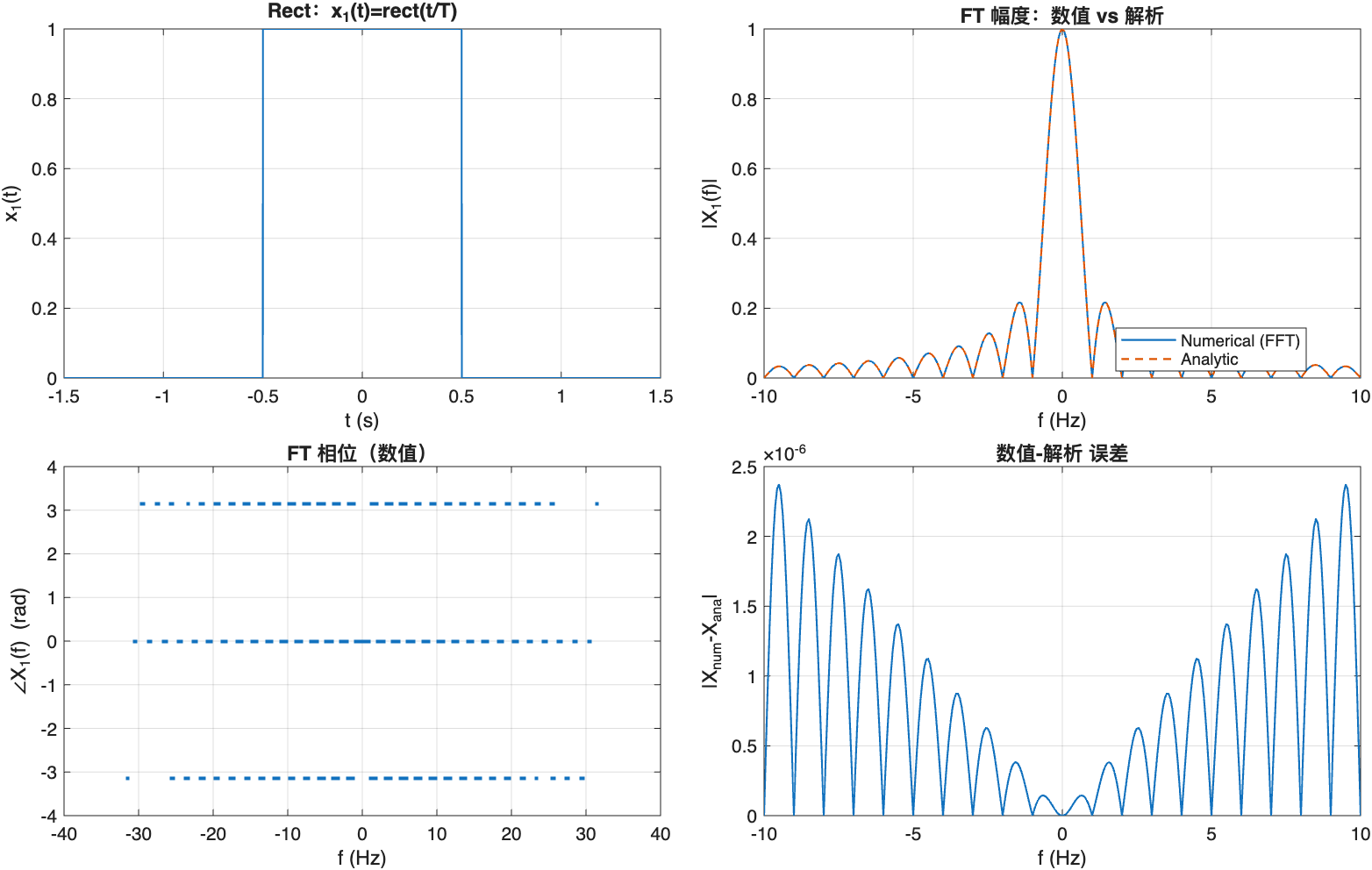

%% --------------------- 示例 2：sinc -> 矩形 ---------------------
Tsinc = 0.25*Trect;               % sinc 的时间尺度，可改
x2 = safe_sinc(t/Tsinc, sincn);    % x2(t) = sinc(t/Tsinc)
X2_num = ctft_fft(x2, dt);         % 数值CTFT近似
% 解析：T * rect(f*T) ；rect(f*T) 的宽度为 1/T
X2_ana = Tsinc * rectp(f, 1/Tsinc);

figure('Name','Sinc <-> Rect','Color','w');
tiledlayout(2,2,"Padding","compact","TileSpacing","compact");

% 时域
nexttile; plot(t, x2, 'LineWidth', 1); grid on;
xlabel('t (s)'); ylabel('x_2(t)'); title('Sinc：x_2(t)=sinc(t/T_s)');
xlim([-6*Tsinc, 6*Tsinc]);

% 频域幅度
nexttile; plot(f, abs(X2_num), 'LineWidth', 1); hold on;
plot(f, abs(X2_ana), '--', 'LineWidth', 1);
grid on; xlabel('f (Hz)'); ylabel('|X_2(f)|');
title('FT 幅度：数值 vs 解析'); legend('Numerical (FFT)','Analytic','Location','best');
xlim([-3/Tsinc, 3/Tsinc]);

% 频域相位（矩形为实非负，解析相位≈0；数值会因截断略波动）
mask2 = abs(X2_ana) > 1e-3*max(abs(X2_ana));
nexttile; plot(f(mask2), angle(X2_num(mask2)), '.', 'MarkerSize', 6); grid on;
xlabel('f (Hz)'); ylabel('∠X_2(f) (rad)'); title('FT 相位（数值）');

% 误差
nexttile; plot(f, abs(X2_num - X2_ana), 'LineWidth', 1); grid on;
xlabel('f (Hz)'); ylabel('|X_{num}-X_{ana}|'); title('数值-解析 误差');
xlim([-3/Tsinc, 3/Tsinc]);

%% ---------- 备注 ----------
% - 增大 L 与 N 可减小截断/采样误差（特别是 sinc 的无限支撑会被时间窗截断）。
% - 若只做DFT演示，可去掉 Δt 标度，此处的 Δt 标度是为了逼近连续型积分定义。
% - 本脚本不依赖专用工具箱；如有 Signal Processing Toolbox，也可用 rectpuls/sinc 直接替代。

%% ===================== 辅助函数 =====================
function [f, df] = make_freq_axis(N, dt)
    df = 1/(N*dt);
    f = ((-N/2):(N/2-1)).' * df;
end

function X = ctft_fft(x, dt)
    % 近似 CTFT：X(f) ≈ Δt * FFTshift( FFT( IFFTshift{x(t)} ) )
    X = fftshift( fft( ifftshift(x) ) ) * dt;
end

function y = safe_sinc(u, sincn)
    % 处理 u=0 处的 0/0
    y = sincn(u);
    y(u==0) = 1;
end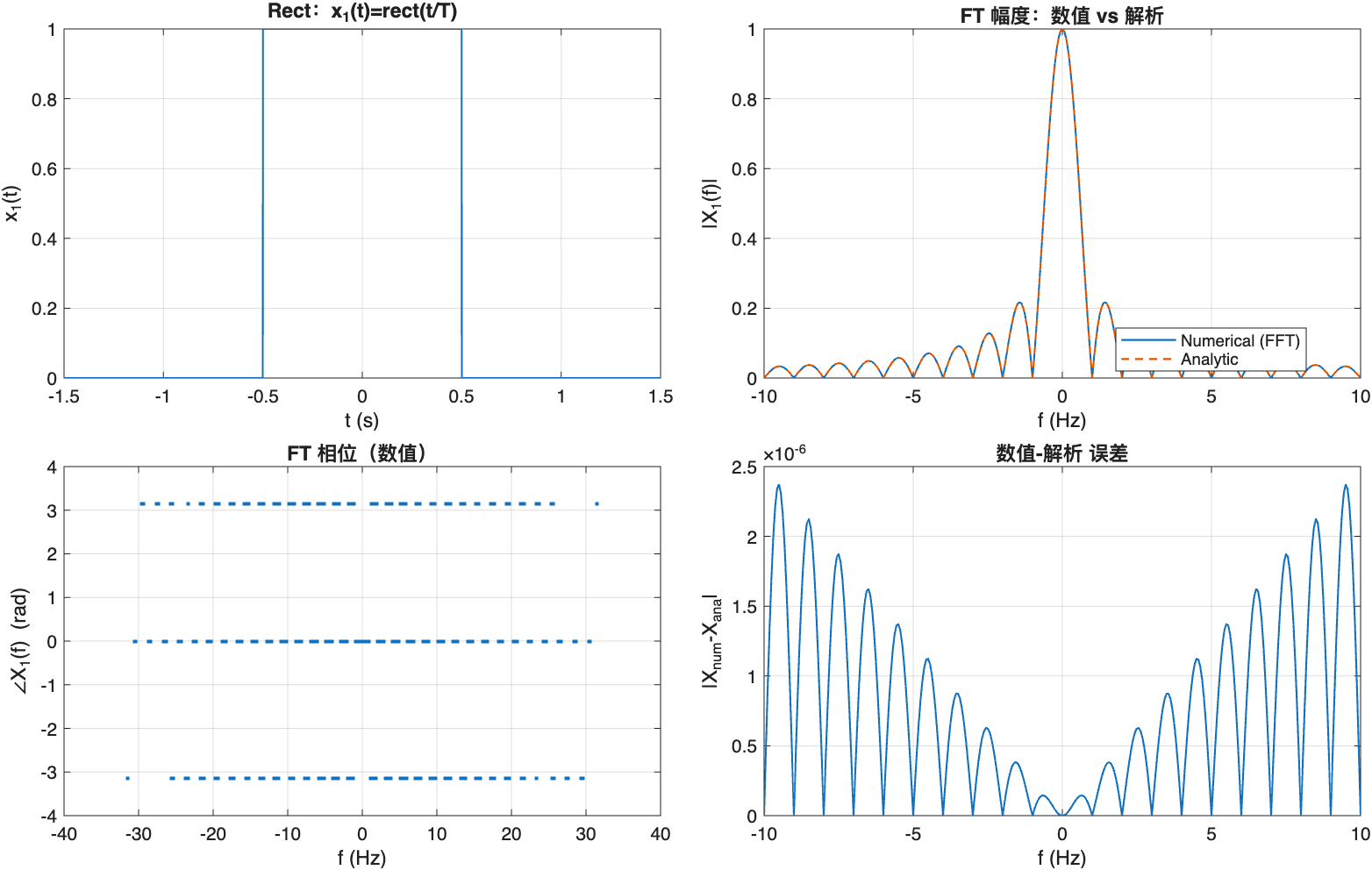

2.4 卷积的离散傅立叶变换计算

弃置点 源自循环卷积卷绕错误的点

补零 为了避免错误输出，将两个序列长度都延拓补零至N=n_1+n_2-1，其中n_1 和n_2 为序列初始长度。

为了提高效率，DFT长度N通常选为2的幂。

2.5 信号采样

采样要求与信号类型有关。

2.5.2 信号类型

实信号与复信号

复解调过程（正交解调）将实信号转换为含有相同信息的复信号。

信号带宽

如果信号的最高频率为f_2，最低（正）频率为f_1，则信号带宽为f_2-f_1。

基本频率范围

指能完整保存信号信息的最低频率集合。

基带和非基带信号

对于实信号，基带信号是指最低正频相对于宽带很小的信号。

对于复信号，基带信号是指在一定的采样率下，连续信号的主要能量完全集中在基本范围内的信号。

2.5.3 奈奎斯特采样率和混叠

实信号采样

奈奎斯特采样率 对于有限带宽的连续基带信号，为使采样能正确描述信号信息，采样率必须高于最高信号频率的两倍，该最小采样率。

非基带实信号

奈奎斯特采样定理 采样率必须高于非基带实信号带宽的两倍。

复信号采样

混叠方程

2.6 平滑窗

2.7 插值

2.7.1 sinc插值

例子一：理想（无限长核）sinc 插值

%% 1) 造一个带限离散信号（两条正弦，最高归一化频率 0.35 cycles/sample < 0.5）
n = -20:20;                   % 离散时间索引
T = 1;                        % 采样周期（先用 1，方便演示）
x = cos(2*pi*0.10*n) + 0.5*sin(2*pi*0.35*n);  % 原离散样本 x[n]

%% 2) 准备要重构的“连续时间”细网格（这里做 16 倍细化）
L = 16;                                        % 细化倍数
t = linspace(n(1), n(end), (numel(n)-1)*L + 1);% 连续时间网格，单位同 n*T

%% 3) 理想 sinc 插值（矢量化实现）
% 公式：x_rec(t) = sum_k x[k] * sinc( (t - k*T)/T )
[tt, nn] = ndgrid(t, n);       % 生成所有 (t, n) 配对
S = sinc((tt - nn*T)/T);       % 权重矩阵（无限长 sinc）
x_rec = S * x(:);              % 对每个 t 做加权求和

%% 4) 可视化
figure; clf
subplot(2,1,1);
stem(n*T, x, 'filled'); hold on; grid on
plot(t, x_rec, 'LineWidth', 1.5);
xlabel('t'); ylabel('幅度');
legend('原始 x[n]','sinc 重构 x(t)');
title('理想 sinc 插值（无限长核）');

%% 5) 和常见插值比较（可选）
subplot(2,1,2);
plot(t, x_rec, 'LineWidth', 1.5); hold on; grid on
x_lin = interp1(n*T, x, t, 'linear');      % 线性插值
x_spl = interp1(n*T, x, t, 'spline');      % 三次样条
plot(t, x_lin, '--');
plot(t, x_spl, ':', 'LineWidth', 1.2);
legend('sinc','linear','spline');
xlabel('t'); ylabel('幅度');
title('不同插值方式对比');

要点说明：

• 这是“数学上的理想重构”，要求已知全体样本（核无限长）。实际中我们只有有限段，因此边缘附近会有误差和振铃（Gibbs-like），图上可见两端略差。

• S*x(:) 是把每个 t 的权重与所有样本做一次内积，因此是 O(N\cdot N_\text{out}) 的计算量，N_out 是细网格点数。

例子二：工程常用的“窗化 + 截断”sinc（有限核）

%% 参数
R = 8;                 % 每侧截断长度（共 2R+1 个 taps）
useWindow = true;      % 是否使用窗函数（Hamming）
% 继续沿用上例中的 n, T, x, t

% 预分配
x_rec_win = zeros(size(t));

% 预先生成窗（对 |k|<=R 的离散 offset）
k = -R:R;
if useWindow
    win = hamming(2*R+1).';     % 行向量
else
    win = ones(1, 2*R+1);
end

% 对每个 t 只与附近 2R+1 个样本相乘求和（简单直观的写法）
for ii = 1:numel(t)
    tc = t(ii)/T;               % 以样本间隔为单位的连续时间
    n0 = floor(tc);             % 最近的样本整数索引
    idx = n0 + k;               % 邻域样本索引
    % 限制索引在有效范围内
    valid = (idx >= n(1)) & (idx <= n(end));
    idxv = idx(valid);

    % 计算对应的 sinc 权重并加窗
    w = sinc( (t(ii) - idxv*T)/T );         % 核
    % 对应的窗系数（按 k 的 valid 子集选择）
    wwin = win(valid);

    % 汇总求和
    xv = x( idxv - n(1) + 1 );              % 取样本值（索引换算）
    x_rec_win(ii) = sum( xv .* w .* wwin );
end

%% 绘图对比
figure; clf; grid on; hold on
plot(t, x_rec, 'LineWidth', 1.5);                 % 无限长（理论参考）
plot(t, x_rec_win, '--', 'LineWidth', 1.5);       % 窗化截断
stem(n*T, x, 'filled');
legend('理想 sinc','窗化截断 sinc','原样本','Location','best');
xlabel('t'); ylabel('幅度');
title(sprintf('窗化截断 sinc（R=%d, %s 窗）', R, ternary(useWindow,'Hamming','Rect')));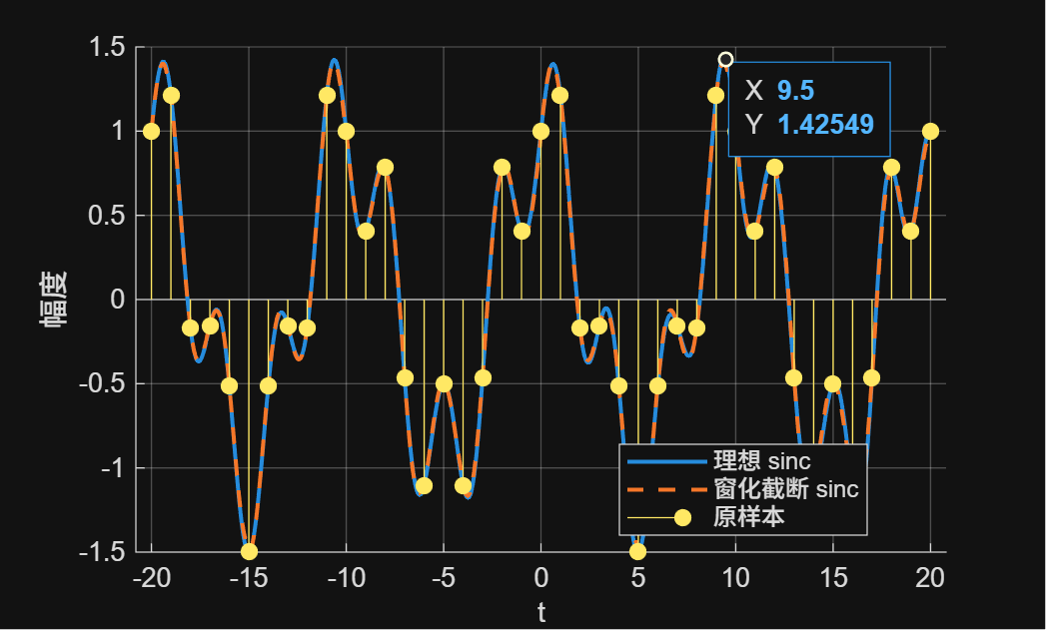

工程实践建议：

• R 取 6–16 通常就很不错；R 越大，越接近理想，但计算量上升。

• 常见窗：Hamming（折中）、Blackman（旁瓣更低）、Kaiser（可调参数 β）。把 win = kaiser(2*R+1, beta).' 即可试不同 β。

• 插值越接近区间中部效果越好，最边缘仍会比理想解差一些（因为缺失“无限远”的样本）。

2.8 点目标分析

峰值旁瓣比（PSLR）最大旁瓣与主瓣的高度比

第三章 线性调频信号的脉冲压缩

3.1 概述

脉冲压缩 一种频谱扩展方法，用于最小化峰值功率、最大化信噪比，以及获得高分辨率目标（如获得高灵敏度的目标检测能力或良好的图像质量）。

3.2 线性调频信号

瞬时频率是时间的线性函数，这种信号用于发射，以得到均匀的信号带宽，其在接受信号中则来自传感器运动。3.2.1 时域表达

当f_{\text{cen}} 为0时，信号的复数形式为s(t)=rect(\frac{t}{T})\exp{{j{\pi}Kt^2}}

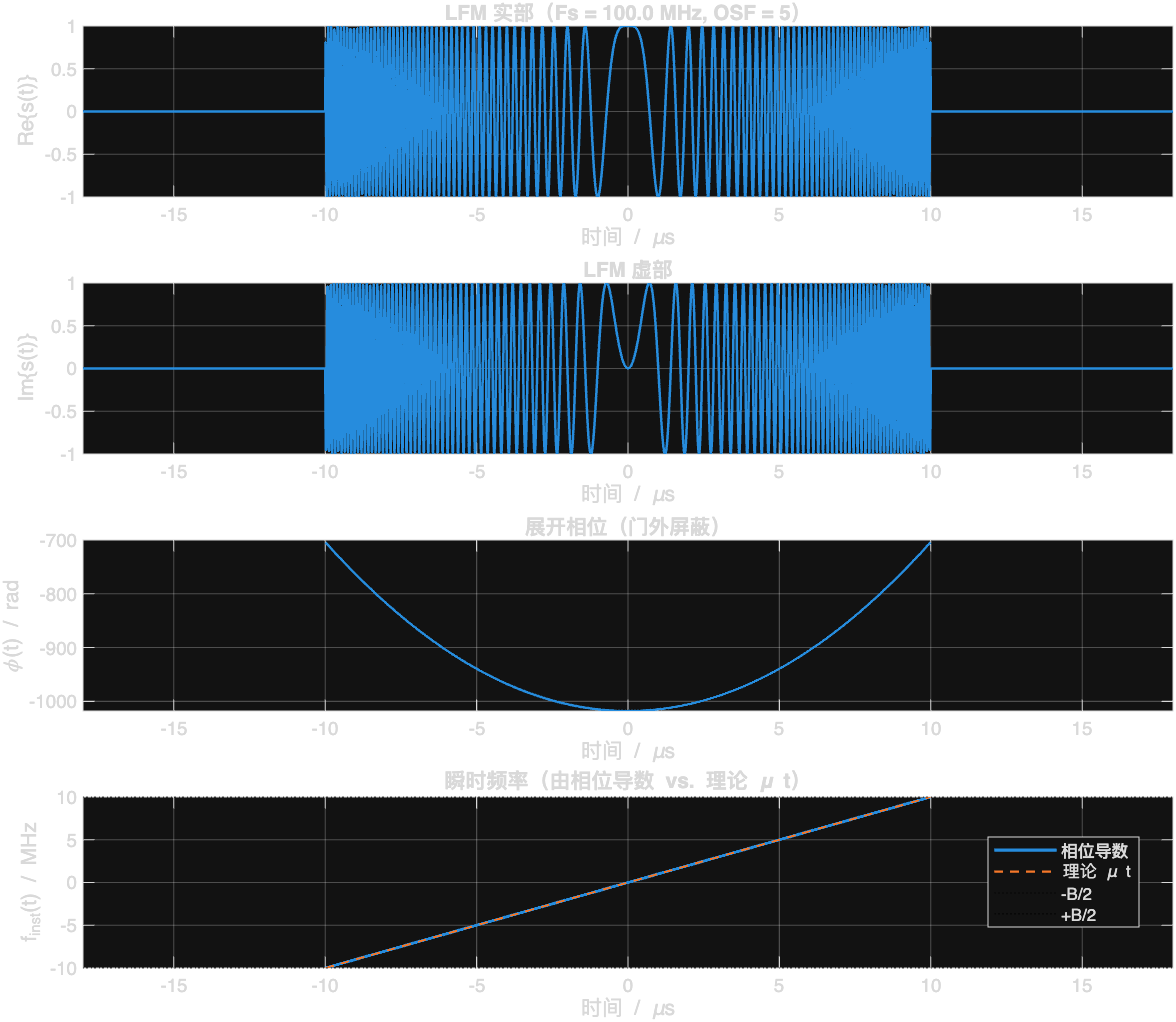
3.2.2 线性调频脉冲的频谱

3.3 脉冲压缩

3.3.1 脉冲压缩原理

如果发射脉冲的持续时间为T，则每一目标在回波数据中占据相同的时间间隔T，故压缩前的可分辨能力为\rho'=T

第四章 合成孔径的概念

SAR信号处理的核心思想：基于对SAR回波信号进行距离向和方位向上的匹配滤波。

4.2 SAR几何关系

4.2.1 术语定义

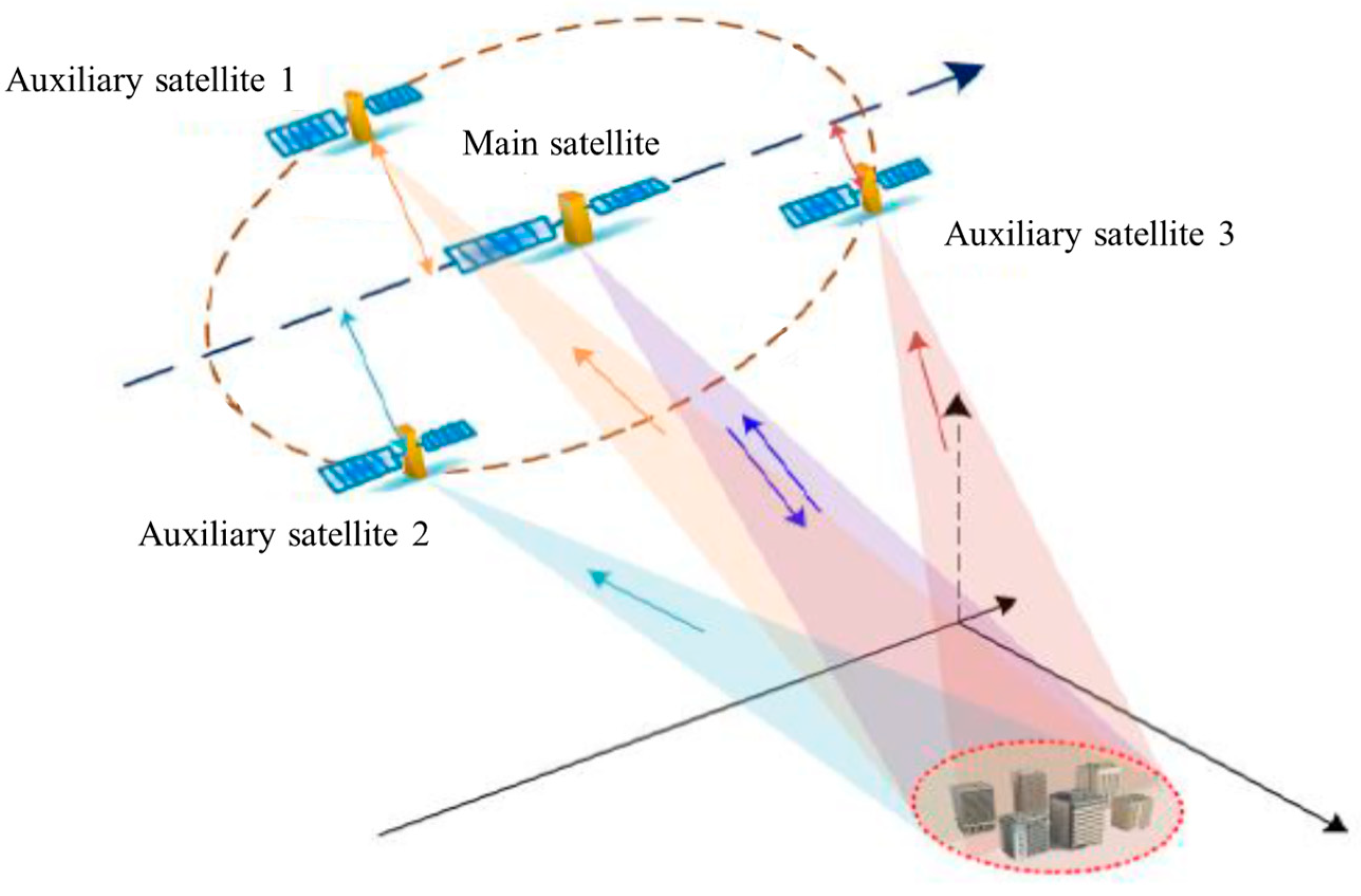
Massonnet 提出的“干涉轮”多基站结构，指的是一种用于星载 SAR 干涉测量的特殊多星座编队构型，一般英文称为 Interferometric Cartwheel / Interferometric Wheel。

以一颗主动发射雷达卫星为中心，在其附近部署若干被动接收小卫星，这些小卫星沿着经过精心设计的椭圆轨道，在主星周围形成类似“轮子”的空间编队，从而在整个轨道周期内获得多条稳定的干涉基线，实现多基线 InSAR。

目标 目标是被SAR照射的地球表面上的一个假想点。

波束覆盖区 在某个脉冲的发射过程中，雷达天线的波束投影到地面的某个区域，称其为波束覆盖区。

星下点 星下点是直接位于传感器下方的地表点，所以星下点至传感器的连线是地球表面的法线。

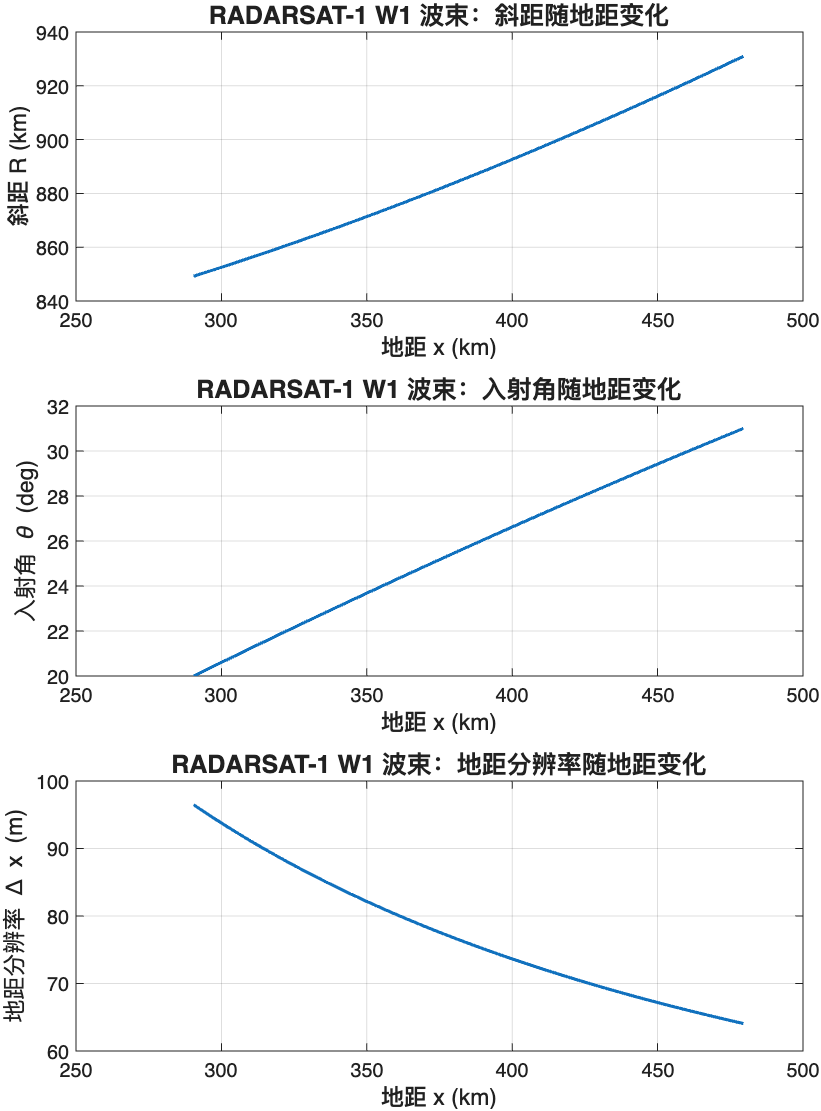
4.2.2 卫星地距几何

在斜距角为零、地球局部近似为球面的情况下，斜距与地距的坐标关系如图所示。

对于特定的雷达模式，斜距采样间隔\Delta R是不变的，而地距采样间隔

随本地入射角而变化。

4.2.3 卫星轨道几何

4.3 距离方程

传感器至目标的斜距是SAR处理中最重要的参数，这个距离随方位向时间而变化，并用所谓的 距离方程 来定义。

注意，不要混淆距离方程和雷达方程式，后者体现的是发射功率和接受SNR的关系。

4.3.1 距离方程的双曲线模型

假设这种简单模型下的速度为V_r，图4.1中的距离X等于V_r \eta，其中\eta为相对于最近点位置的方位向时间。那么，根据毕达哥拉斯定律，传感器到目标点的距离R(\eta)由如下双曲模型方程给出：

其中R_0为雷达离目标最近时的斜距，即最短距离。

4.3.2 速度与角度的关系

对于典型星载情况，\theta_r约比\theta_{sq}大6%，即使在斜视角为6度时两者的余弦值之差也不会超过0.08%。

4.4 SAR距离向信号

4.4.1 发射脉冲

在距离向，雷达发射的调制脉冲为

其中\tau为距离向时间，P_n是当信号相位以幂级数表示时的相位系数。

4.4.2 数据获取

考察距雷达R_a处的一个点目标，其后向散射系数\sigma_0的幅度为A_0'，则式（4.25）中的g_r(\tau)=A_0'\delta(\tau-2R_a/c)，其中2R_a/c 为该点的信号延时。由式（4.21）和式（4.25）可知，该目标点的接收信号为

上式中，\psi表示地表散射过程可能引起的雷达信号相位改变。对于特定的反射体，只要在雷达照射时间内其相位变化为常数，前述分析就仍然适用。

4.5 SAR方位向信号

4.5.1 什么是SAR中的多普勒频率

在上面的讨论中忽略了以下几点：

1. 雷达产生和发射的是一个有限时宽的脉冲，而不是一个单频波。

2. 雷达电子设备将脉冲上变频到非常高的频率（雷达载频），然后将接收信号下变频到初始频率（或更低的基带）。

3. 脉冲具有线性调频波形而不是单频的，并且经过接收和下变频后，信号被转换（压缩）为一个近似sinc函数的尖脉冲。

4.5.2 相干脉冲

相干脉冲具有均匀的间隔，如图4.8所示，每个脉冲用式（4.19）或式（4.21）表示。“相干”意味着每个脉冲的起始时间和相位都受到精确的控制。接收机和解调器同样要具有很高的时间精度。

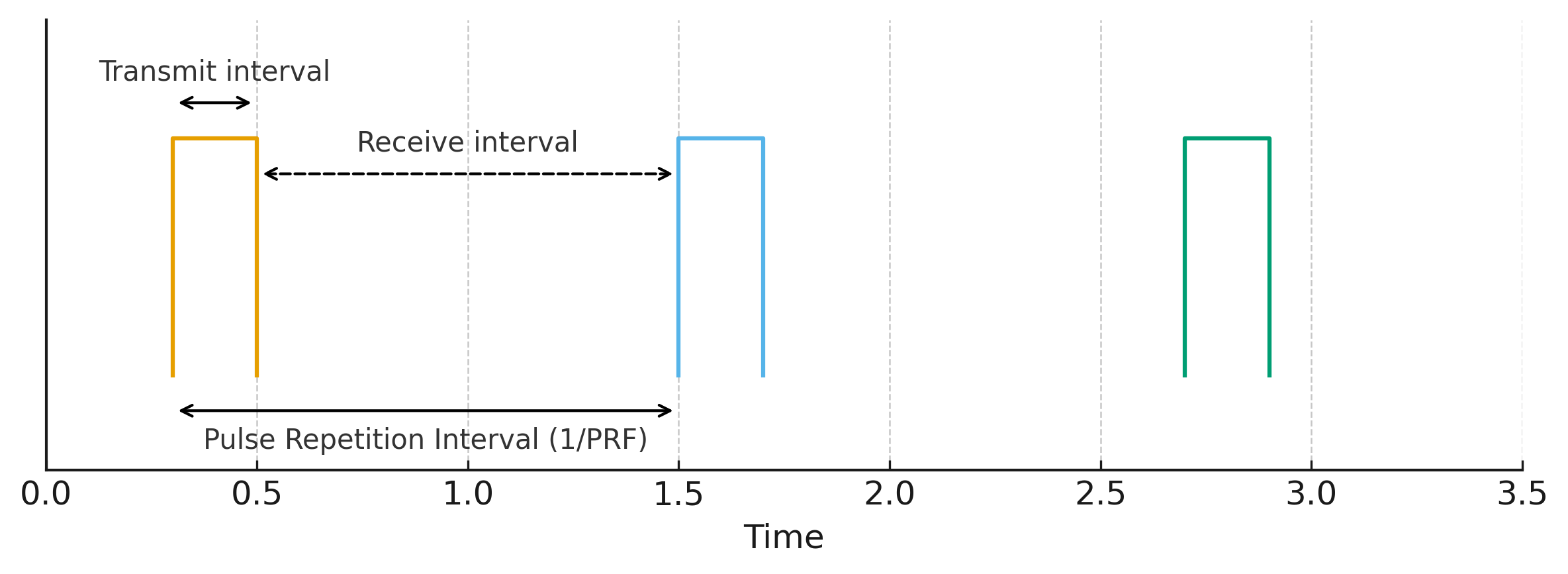
当雷达不处于发射状态时，它接收地物反射回波。发射脉冲和接收回波的时间序列如图4.9所示。在机载情况下，每个回波可以在脉冲发射间隔内直接接收到。但是在星载情况下，由于距离过大，某个脉冲的回波要经过6～10个脉冲间隔才能接收到。

4.5.3 PRF的选择

选择方位向采样率（或PRF）需要考虑下列参数和准则。

奈奎斯特采样率 由于是复采样，PRF应大于方位信号带宽的主要部分。

距离测绘带宽度 采样窗时间上限为1/PRF-T_r秒，相应的斜距间隔为(1/PRF-T_r)c/2m。

接收窗时序 在某发射脉冲的回波需要经过几个脉冲间隔才能被接收到的星载情况下，这一起始时间尤其受到PRF的影响。

星下点回波 因为星下点回波也是距离模糊，因而这一能量是星载SAR应尽量避免的，通常会选择合适的PRF，使星下点回波不落在接收窗之内（或者至少不落在主要成像带之内）。

4.5.4 方位向信号强度和多普勒历程

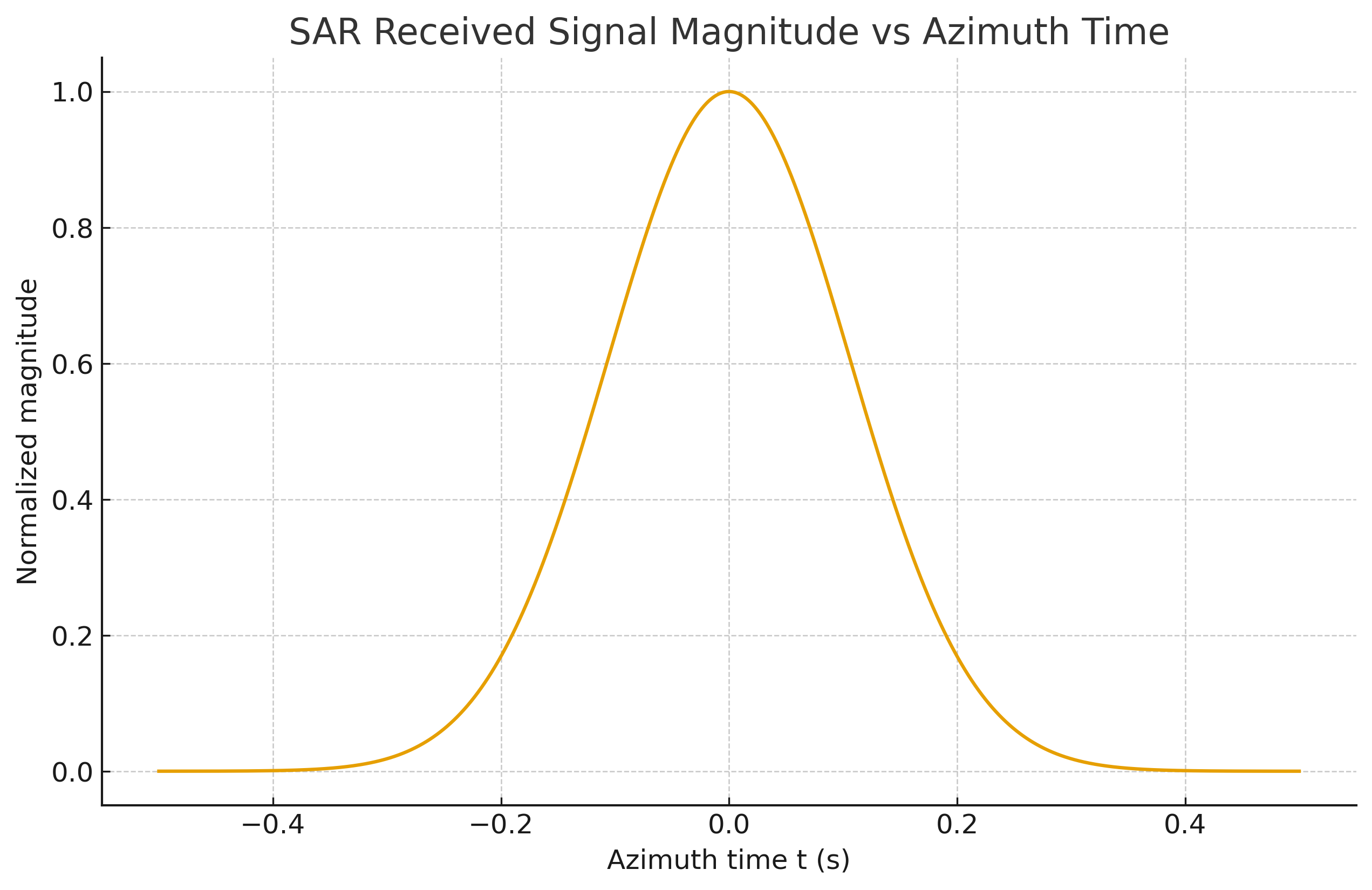
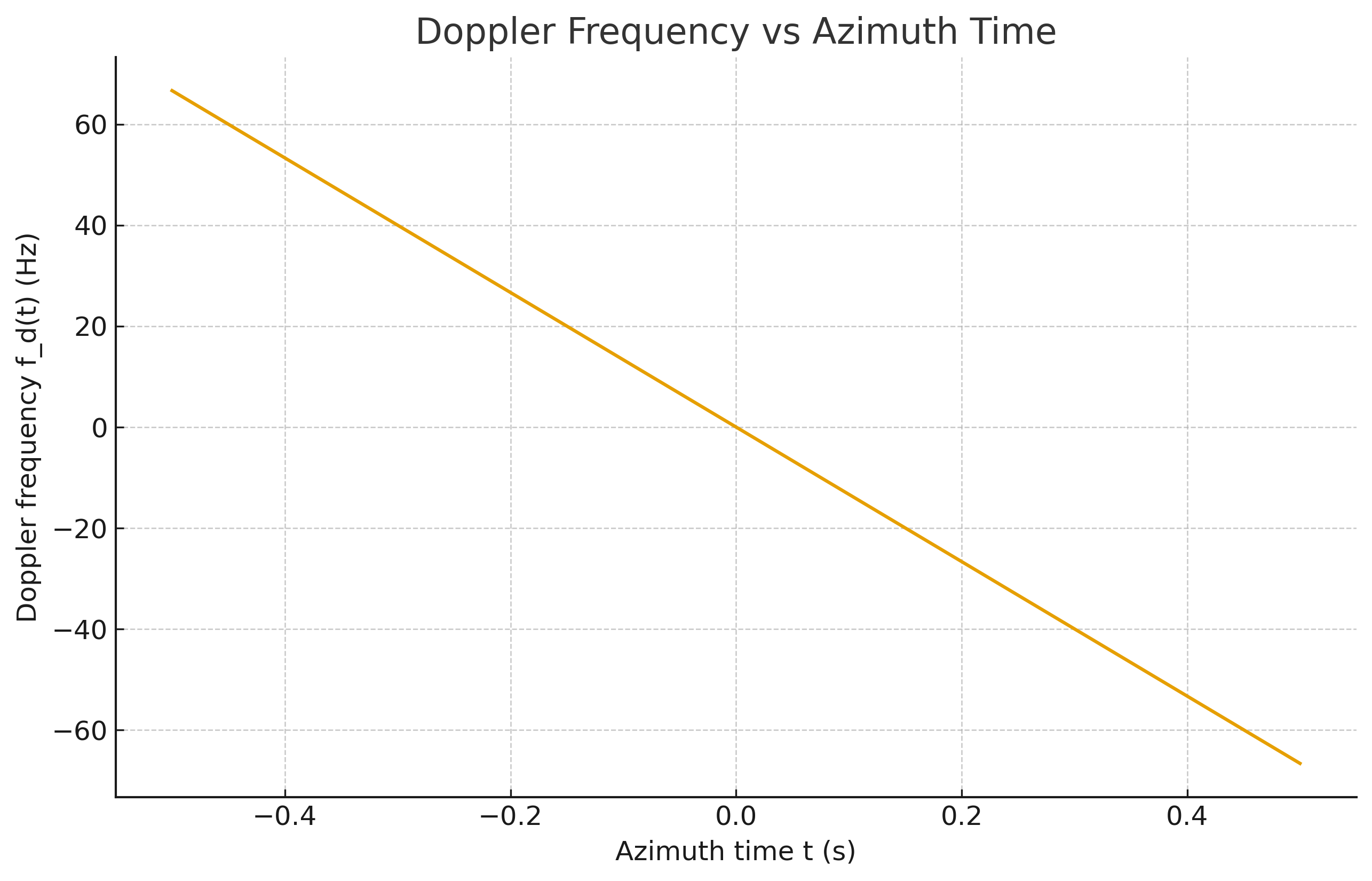
多普勒频率正比于目标相对于传感器的径向速度。当目标接近雷达时多普勒频率为正，当目标远离雷达时多普勒频率为负，因此频率随时间变化曲线的斜率为负。

由于雷达能量的双程传播过程，接收信号的强度由p_a(\theta)的平方给出，并且通常可以表示成方位向时间\eta的函数

式（4.11）表明了\theta_{sq}与方位向时间\eta的关系。

在一般的非零斜视角情况下，波束中心在被称为“波束中心穿越时刻”的时间点经过目标，以零多普勒时间作为参考，该时刻记为\eta_c。按照前文习惯，当波束前视时，\eta_c为负，当波束后视时，\eta_c为正。\eta_c可表示为

其中R(\eta_c)为目标被波束中心照射时的雷达距目标的斜距，\theta_{sq,c}为该时刻的\theta_{sq}值。

在这种斜视情况下，式（4.27）中的与视线的夹角\theta等于\theta_{sq}-\theta_{sq,c}。利用小角度近似，双程波束方向图为

即等于式（4.28）中的\omega_a(\eta-\eta_c)。

基于以上讨论，式（4.26）中的R_a是随时间\eta变化的，表示为R(\eta)。点目标接收信号可以写成

这是点目标接收信号的实数表达式，R_0为最短距离，距离R(\eta)由式（4.9）给出。

4.5.5 方位向参数

多普勒中心频率

\eta=\eta_c处的多普勒中心频率正比于式（4.9）中R(\eta)的变化率，

单位为Hz。上式的推导用到了式（4.13）。

多普勒带宽

根据式（4.33），目标的方位向带宽为

其中比例系数V_s/V_r源自直线几何假设。

目标照射时间

照射时间是目标处于3dB波束范围内的时间宽度，可写为

其中0.886\lambda/L_a为方位向波束宽度，因此0.886R(\eta_c)\lambda/L_a为波束宽度在地面上的投影。

方位向调频率

方位向调频率是方位向频率或多普勒频率的变化率，

其中方位向频率为2/\lambda乘以距离的一阶导数。

4.6 二维信号

4.6.1 信号存储器中的数据排列

第五章 SAR信号的性质

5.2 低斜视角情况下的信号频谱

5.2.1 距离多普勒频谱

忽略常数项乘积，距离多普勒域中的信号可表示为

其中R_{rd}为该御中的距离徙动。

5.2.2 二维频谱

忽略常数项乘积，二维频域中的信号形式为

注意，距离向频率包络W_r只是f_\tau的函数而不是f_\eta的函数，故目标徙动轨迹并不体现在W_r上，而是隐藏在式（5.11）中的相位\theta_{2df}里。

5.3 一般情况下的信号频谱

5.3.1 距离向多普勒变换

5.4 方位混叠与多普勒中心

5.4.1 方位混叠和模糊的起因

如4.5.3节所述，方位向采样率PRF的提高常常会受到诸如距离测绘带等因素的限制。这意味着方位信号分量将以模糊的形式相互混叠，这一问题将在随后的两节中讨论。

%% 离散脉冲对方位信号的采样造成的方位混叠
clear; clc; close all;

%% ------------ 基本参数设置 ------------ %%
PRF2 = 1000;              % 低 PRF（产生混叠），单位：Hz
PRF1 = 4 * PRF2;          % 高 PRF（混叠前），单位：Hz，设为低 PRF 的 4 倍

T_az = 0.128;             % 方位向观测时间长度（秒）
N1   = round(PRF1*T_az);  % 高 PRF 下采样点数
N2   = round(PRF2*T_az);  % 低 PRF 下采样点数

% 将时间轴中心对齐到 0，便于看到对称的 chirp
t1 = ((0:N1-1) - N1/2)/PRF1;   % 高 PRF 的时间轴
t2 = ((0:N2-1) - N2/2)/PRF2;   % 低 PRF 的时间轴

% 方位向 chirp 参数：f_inst(t) = f0 + K * t
f0 = 0;                 % 中心频率（相对基带），Hz
K  = 2e4;               % 方位向频率调制斜率（Hz/s），保证在高 PRF 下不混叠，在低 PRF 下混叠

% 连续时间相位：phi(t) = 2*pi * (f0*t + 0.5*K*t^2)
phi1 = 2*pi*(f0*t1 + 0.5*K*t1.^2);
phi2 = 2*pi*(f0*t2 + 0.5*K*t2.^2);

% ------------ (a) 混叠前 chirp 信号（高 PRF 采样） ------------ %
s1 = real(exp(1j*phi1));   % 取实部作为方位向回波实部

% ------------ (b) 混叠后 chirp 信号（低 PRF 采样） ------------ %
s2 = real(exp(1j*phi2));   % 同一物理信号，在低 PRF 下采样，产生多普勒混叠

% ------------ (c) 瞬时频率（归一化到低 PRF） ------------ %
% 真实瞬时频率（Hz）
f_inst_true = f0 + K*t2;        % 与物理场景有关的真实方位向多普勒频率

% 归一化到低 PRF（单位：PRF2 的倍数）
f_norm_true = f_inst_true / PRF2;

% 数字角频率 (rad/sample)，按低 PRF 计算
omega2 = 2*pi*f_inst_true / PRF2;

% 利用 atan2(sin, cos) 将角频率折叠到 [-pi, pi]，体现混叠
omega2_alias = atan2(sin(omega2), cos(omega2));

% 折叠后的归一化频率（相对于 PRF2），范围约在 [-0.5, 0.5]
f_norm_alias = omega2_alias / (2*pi);

%% ------------ 画图 ------------ %%
figure('Position',[200 100 900 700],'Color','w');

% (a) 混叠前方位 chirp 信号实部（高 PRF）
subplot(3,1,1);
n1 = 0:N1-1;   % 方位向采样点序号
plot(n1, s1, 'LineWidth', 1.2);
grid on;
xlabel('方位向（采样点）');
ylabel('幅度');
title('（a）混叠前方位 chirp 信号实部（高 PRF 采样）');

% (b) 混叠后方位 chirp 信号实部（低 PRF）
subplot(3,1,2);
n2 = 0:N2-1;   % 方位向采样点序号
plot(n2, s2, 'LineWidth', 1.2);
grid on;
xlabel('方位向（采样点）');
ylabel('幅度');
title('（b）混叠后方位 chirp 信号实部（低 PRF 采样）');

% (c) 瞬时频率（虚线：真实频率 / PRF2；实线：混叠后频率 / PRF2）
subplot(3,1,3);
plot(n2, f_norm_true, '--', 'LineWidth', 1.5); hold on;
plot(n2, f_norm_alias, '-',  'LineWidth', 1.5);
grid on;
xlabel('方位向（采样点）');
ylabel('瞬时频率 / PRF');
title('（c）瞬时频率：虚线为真实频率，实线为采样后混叠频率');
legend('真实瞬时频率 / PRF','混叠后频率 / PRF','Location','best');

% 总标题
sgtitle('离散脉冲对方位信号的采样造成的方位混叠');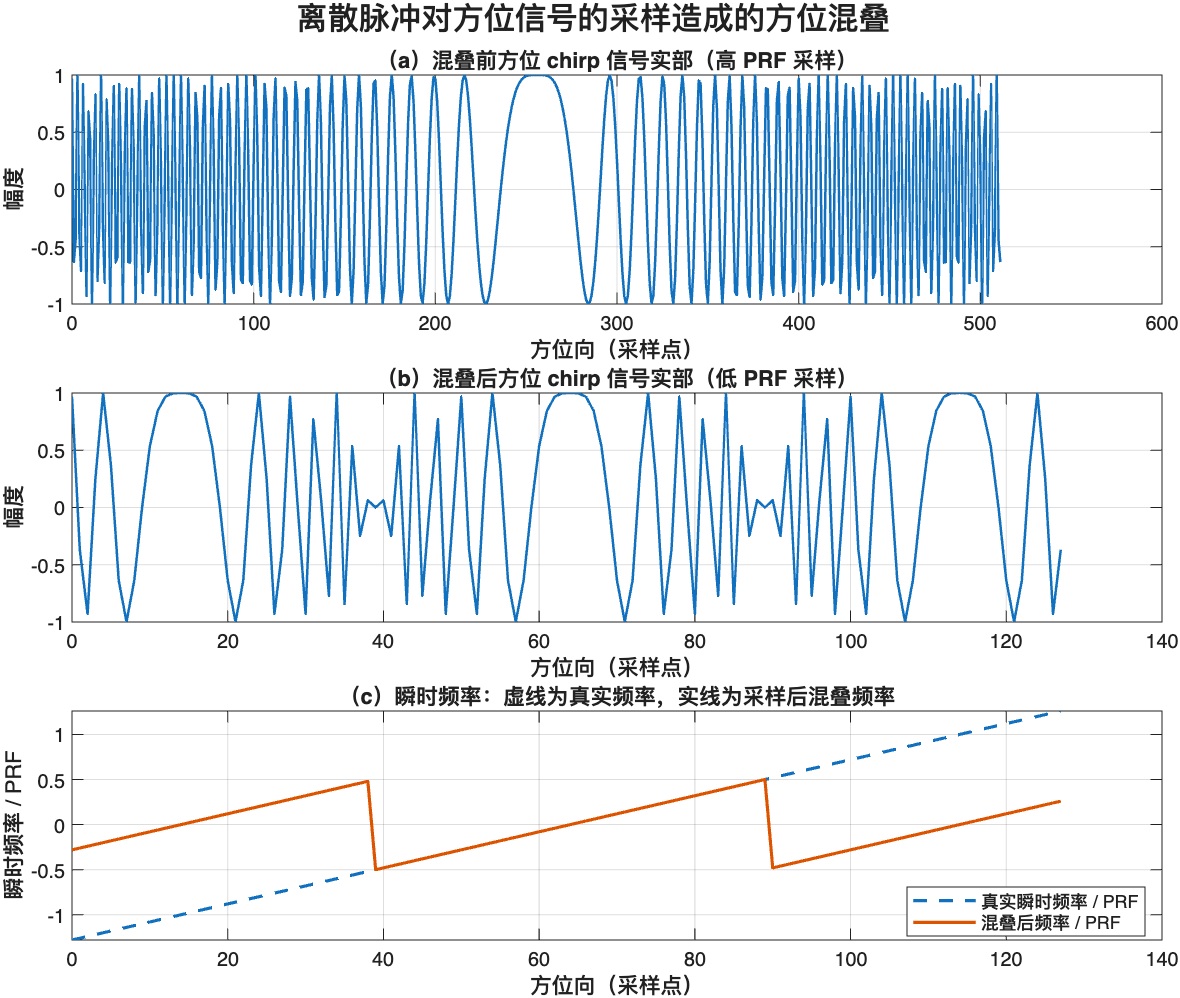

当对信号频率进行观测时，混叠现象也会变得很明显。在图5.3（c）中，虚线表示图5.3（a）中没有混叠的信号频率，实线表示图5.3（b）中降采样信号或混叠信号的频率。

PRF时间定义为覆盖一个PRF频带的方位chirp信号时间，在图5.3中，就是32个采样时间。PRF时间的引入是为了强调由雷达系统PRF采样造成的混叠现象。

5.4.2 多普勒中心

实际上，如图5.4所示，点目标接收信号能量只集中在一个PRF时间内。信号幅度受到方位向波束形状的调制，这种调制使峰值出现在某一频率点上，而-6dB（双程）基准出现在距峰值频率点两侧略小于PRF/2时间处。

多普勒模糊 由于可能存在方位混叠，从方位频谱中观测到的多普勒中心并不唯一。当实际中心频率并不处于观测频谱的基带(-F_a/2,+F_a/2)之内时，就会发生模糊。

5.4.3 多普勒模糊

由于信号的PRF采样，频谱是混叠的。“基带”频谱是接收数据中唯一可见的频谱。通过观测频谱的峰值位置估计出的多普勒中心频率处于\pm0.5F_a范围内，其中F_a为PRF。由于观测到的多普勒中心频率局限于一个PRF之内，将其称为多普勒中心的小数PRF部分，用符号f'_{\eta_c}表示，以与绝对多普勒中心频率区别开。

5.4.4 距离向的多普勒中心变化

在距离频域的处理算法中，一个距离处理带宽内的多普勒中心变化不能太大。如果变化过大，而PRF又不够高，那么位于方位谱起始和结束位置处的能量会互相混合，方位模糊就会加重。

5.5 距离徙动

5.5.1 距离徙动的分量

5.5.2 同一距离处的多个目标

5.5.3 目标轨迹卷绕

5.6 点目标示例

5.6.1 仿真参数

5.7 SAR处理算法初窥

5.7.1 时域匹配滤波

5.7.2 机载实时处理图像

5.7.3 非聚焦SAR

5.7.4 更好的处理算法