一、定义和术语

MATLAB函数“pulse_train.m”

function [dt, prf, pav, ep, ru] = pulse_train(tau, pri, p_peak)
% computes duty cycle, average transmitted power, pulse energy, and pulse repetition frequency
% Inputs:
    %   tau    == Pulsewidth in seconds
    %   pri    == Pulse repetition interval in seconds
    %   p_peak == Peak power in Watts
%
% Outputs:
    %   dt    == Duty cycle - unitless
    %   prf   == Pulse repetition frequency in Hz
    %   pa    == Average power in Watts
    %   ep    == Pulse energy in Joules
    %   ru    == Unambiguous range in Km
%
c = 3e8; % speed of light
dt = tau / pri;
prf = 1. / pri;
pav = p_peak * dt;
ep = p_peak * tau;
ru = 1.e-3 * c * pri /2.0;
return

MATLAB函数“pulse_train.m”计算占空因子、平均发射功率、脉冲能量和脉冲重复频率。语法如下：

[dt,pav,ep,prf,ru]=pulse_train(tau,pri,p_peak)

其中：

符号	说明	单位	状态
tau	脉冲宽度	s	输入
pri	PRI	s	输入
p_peak	峰值功率	W	输入
dt	占空因子	无	输出
pav	平均发射功率	W	输出
ep	脉冲能量	J	输出
prf	PRF	Hz	输出
ru	非模糊距离	km	输出

MATLAB函数“range_resolution.m”

function [delta_R] = range_resolution(var)
% This function computes radar range resolution in meters
%
% Inputs:
    % var can be either
        % var == Bandwidth in Hz
        % var == Pulsewidth in seconds
%    
% Outputs:
    % delta_R == range resolution in meters
%    
% Bandwidth may be equal to (1/pulse width)==> indicator = seconds
%
c = 3.e+8; % speed of light
indicator = input('Enter 1 for var == Bandwidth, OR 2 for var == Pulsewidth \n');
switch(indicator)
    case 1
        delta_R = c / 2.0 / var; % del_r = c/2B
    case 2
        delta_R = c * var / 2.0; % del_r = c*tau/2
end
return

MATLAB函数“range_resolution.m“计算距离分辨率。语法如下：

[delta_R]=range_resolution(var,indicator)

其中：

符号	说明	单位	状态
var,indicator	带宽，“hz“	Hz，无	输入
var,indicator	脉冲宽度，“s”	s，无	输入
delta_R	距离分辨率	m	输出

例：

非模糊距离为100km的雷达系统，带宽为0.5MHz。计算需要的PRF、PRI、\Delta R和\tau。

解：

PRF=\frac{c}{2R_u}=\frac{3\times10^8}{2\times10^5}=15

PRI=\frac{1}{PRF}=\frac{1}{1500}=0.6667ms

使用函数“range_resolution”，得

\Delta R=\frac{c}{2B}=\frac{3\times10^8}{2\times0.5\times10^6}=300m

\tau = \frac{2\Delta R}{c}=\frac{2\times300}{3\times10^8}=2\mu s

MATLAB函数“droppler_freq.m”

function [fd, tdr] = doppler_freq (freq, ang, tv)
% This function computes Doppler frequency and time dilation factor ratio
% tau_prime / tau
% 
% Inputs:
    % freq  == radar operating frequency in Hz
    % ang   == target aspect angle in degrees
    % tv    == target velocity in m/sec
%    
% Outputs:
    % fd    == Doppler frequency in Hz
    % tdr   == time dilation factor; unitless
%
format long
indicator = input('Enter 1 for closing target, OR 2 for opening target \n');
c = 3.0e+8;
ang_rad = ang * pi /180.;
lambda = c / freq;
switch(indicator)
    case 1
        fd = 2.0 * tv * cos(ang_rad) / lambda;
        tdr = (c - tv) / (c + tv);
    case 2
        fd = -2.0 * c * tv * cos(and_rad) / lambda;
        tdr = (c + tv) / (c -tv);
end
return

函数“droppler_freq.m“计算多普勒频率。语法如下：

[fd,tdr]=doppler_freq(freq,ang,tv,indicator)

其中：

符号	说明	单位	状态
freq	雷达工作频率	Hz	输入
ang	姿态角	度	输入
tv	目标速度	m/s	输入
fd	多普勒频率	Hz	输出
tdr	时间扩张因子比\tau'/\tau	无	输出

二、基本脉冲和连续波（CW）雷达操作

MATLAB函数“radar_eq.m”

function [snr] = radar_eq(pt, freq, g, sigma, b, nf, loss, range)
% This function implements Eq. (2.22) of textbook
%
% Inputs:
        % pt        == input peak power in Watts
        % freq      == radar operating frequency in Hz
        % g         == antenna gain in dB
        % sigma     == radar cross section in meter squared
        % b         == radar bandwidth in Hz
        % nf        == noise Figure in dB
        % loss      == total radar losses in dB
        % range     == range to target (single value or vector) in Km
%    
% Outputs:
        % snr       == SNR in dB     
% 
c = 3.0e+8; % speed of light
lambda = c / freq; % wavelength
p_peak = 10*log10(pt); % convert peak power to dB
lambda_sqdb = 10*log10(lambda^2); % compute wavelength square in dB
sigmadb = 10*log10(sigma); % convert sigma to dB
four_pi_cub = 10*log10((4.0 * pi)^3); % (4pi)^3 in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
to_db = 10*log10(290); % noise temp. in dB
b_db = 10*log10(b); % bandwidth in dB
range_pwr4_db = 10*log10(range.^4); % vector of target range^4 in dB
% Implement Equation (2.22)
num = p_peak + g + g + lambda_sqdb + sigmadb;
den = four_pi_cub + k_db + to_db + b_db + nf + loss + range_pwr4_db;
snr = num - den;
return

函数“radar_eq.m”执行方程（2.22），语法如下：

[snr]=radar_eq(pt,freq,g,sigma,b,nf,loss,range)

(SNR)_0=\frac{P_tG^2\lambda^2\sigma}{(4\pi)^3kT_sBLR^4}

其中：

符号	说明	单位	状态
pt	峰值功率	W	输入
freq	雷达中心频率	Hz	输入
g	天线增益	dB	输入
sigma	目标截面积	m²	输入
b	带宽	Hz	输入
nf	噪声系数	dB	输入
loss	雷达损耗	dB	输入
range	目标距离（可以是一个单值或一个向量）	m	输入
snr	SNR（单值或者向量，取决于目标距离）	dB	输出

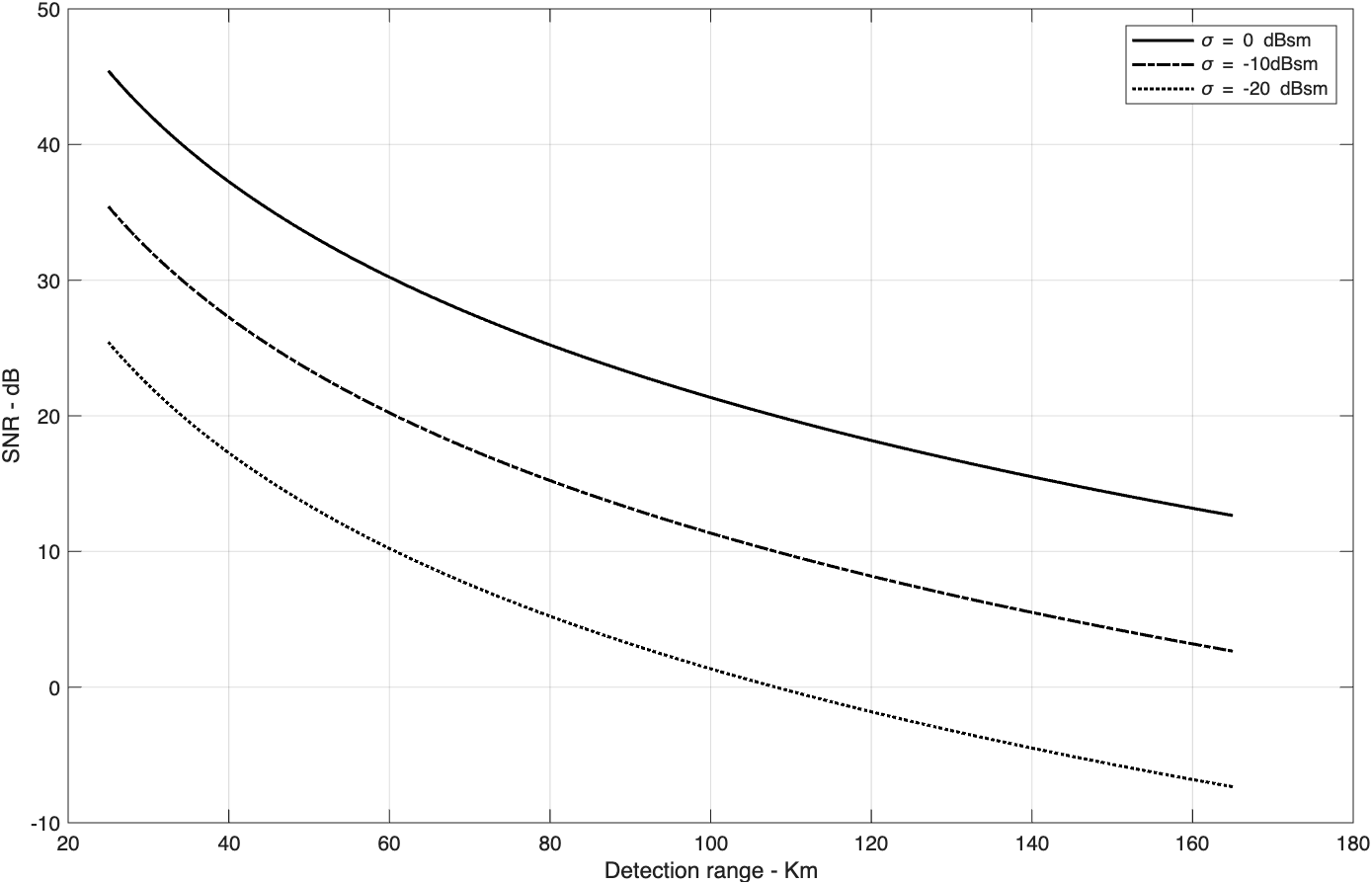
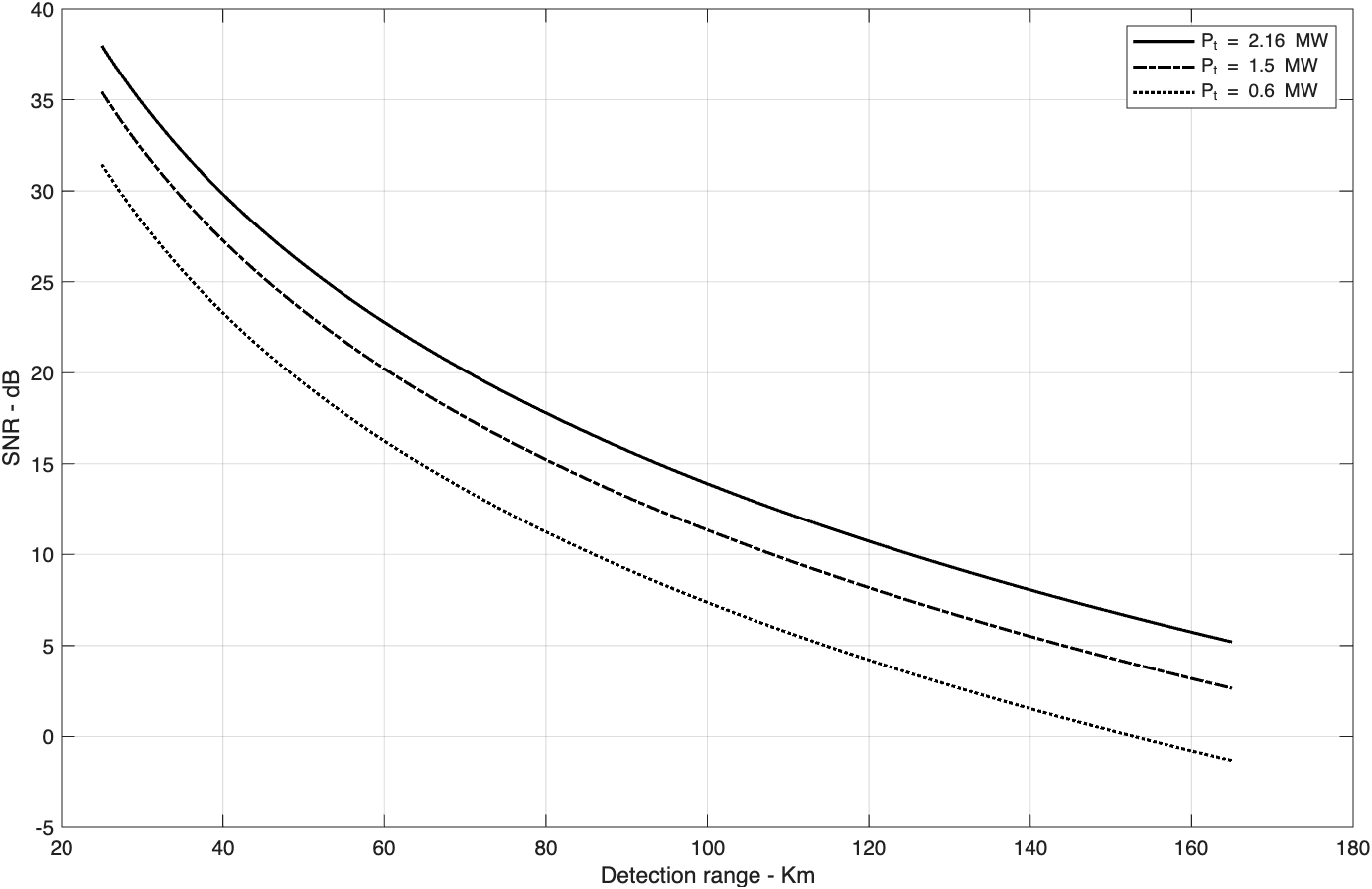
函数“radar_eq.m”设计成可以接受一个单值的输入“range”，或一个包含很多距离值的向量。图2.1给出了使用以下输入值得到的典型曲线：峰值功率P_t=1.5MW，工作频率f_0=5.6GHz，天线增益G=45dB，雷达损耗L=6dB，噪声系数F=3dB。雷达带宽B=5MHz。雷达最小和最大探测距离是R_{min}=25km和R_{max}=165km。

MATLAB函数“lprf_req.m”

function [snr] = lprf_req(pt, g, freq, sigma, np, b, nf, loss, range)
% This program implements Eq. (2.27) of textbook
%
% Inputs:
        % pt        == input peak power in Watts
        % freq      == radar operating frequency in Hz
        % g         == antenna gain in dB
        % sigma     == radar cross section in meter squared
        % b         == radar bandwidth in Hz
        % nf        == noise Figure in dB
        % np        == number of pulses
        % loss      == total radar losses in dB
        % range     == range to target (single value or vector) in Km
%    
% Outputs:
        % snr       == SNR in dB     
% 
c = 3.0e+8; % speed of light
lambda = c / freq; % wavelength
p_peak = 10*log10(pt); % convert peak power to dB
lambda_sqdb = 10*log10(lambda^2); % compute wavelength square in dB
sigmadb = 10*log10(sigma); % convert sigma to dB
four_pi_cub = 10*log10((4.0 * pi)^3); % (4pi)^3 in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
to_db = 10*log10(290); % noise temp. in dB
b_db = 10*log10(b); % bandwidth in dB
np_db = 10.*log10(np); % number of pulses in dB
range_pwr4_db = 10*log10(range.^4); % vector of target range^4 in dB
% Implement Equation (1.68)
num = p_peak + g + g + lambda_sqdb + sigmadb + np_db;
den = four_pi_cub + k_db + to_db + b_db + nf + loss + range_pwr4_db;
snr = num - den;
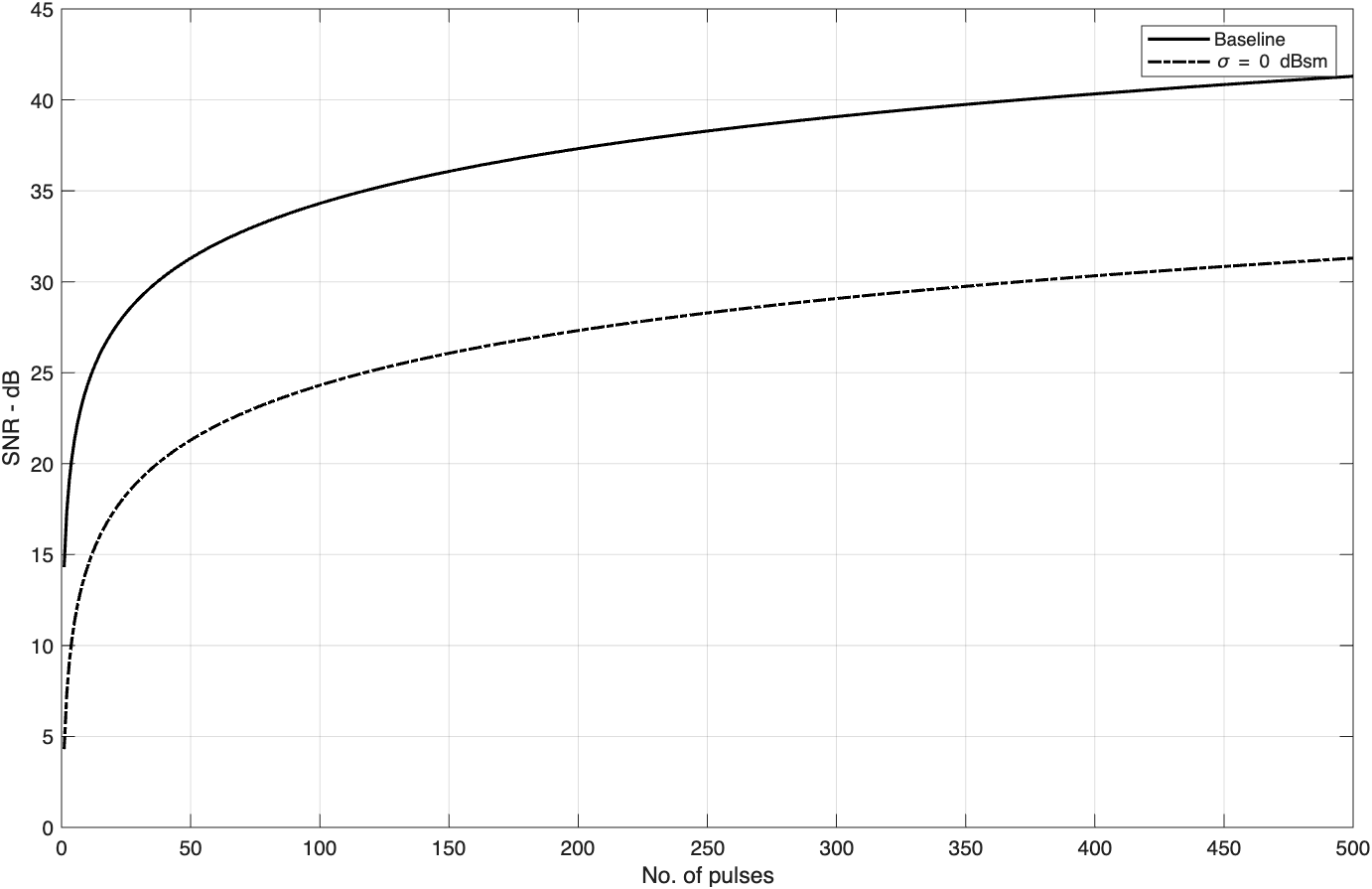
return

函数“lprf_req.m”执行方程（2.27）给出的低PRF下的雷达方程。对于给定的一组输入参数，函数“lprf.m”计算(SNR)_{n_p}。语法如下：

[snr]=lprf_req(pt,g,freq,sigma,np,b,nf,loss,range)

其中：

符号	说明	单位	状态
pt	峰值功率	W	输入
g	天线增益	dB	输入
freq	频率	Hz	输入
sigma	目标截面积	m²	输入
np	脉冲个数	无	输入
b	带宽	Hz	输入
nf	噪声系数	dB	输入
loss	雷达损耗	dB	输入
range	目标距离（可以是单值或向量）	km	输入
snr	SNR（可以是单值或向量）	dB	输出

图2.2给出用函数“lprf_req.m”产生的典型曲线，采用的输入：峰值功率P_t=1.5MW，工作频率f_0=5.6GHz，天线增益G=45dB，雷达损耗L=6dB，噪声系数F=3dB。雷达带宽B=5MHz。目标RCS为\sigma=0.1m^2。

MATLAB函数“hprf_req.m”

function [snr] = hprf_req (pt, Ti, g, freq, sigma, dt, range, nf, loss)
% This program implements Eq. (2.31)of textbook
%
% Inputs:
        % pt        == input peak power in Watts
        % freq      == radar operating frequency in Hz
        % g         == antenna gain in dB
        % sigma     == radar cross section in meter squared
        % Ti        == time on target in seconds
        % nf        == noise Figure in dB
        % dt        == duty cycle
        % loss      == total radar losses in dB
        % range     == range to target (single value or vector) in Km
%    
% Outputs:
        % snr       == SNR in dB     
% 
c = 3.0e+8; % speed of light
lambda = c / freq; % wavelength
pav = 10*log10(pt*dt); % compute average power in dB
Ti_db = 10*log10(Ti); % time on target in dB
lambda_sqdb = 10*log10(lambda^2); % compute wavelength square in dB
sigmadb = 10*log10(sigma); % convert sigma to dB
four_pi_cub = 10*log10((4.0 * pi)^3); % (4pi)^3 in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
to_db = 10*log10(290); % noise temp. in dB
range_pwr4_db = 10*log10(range.^4); % vector of target range^4 in dB
% Implement Equation (1.72)
num = pav + Ti_db + g + g + lambda_sqdb + sigmadb;
den = four_pi_cub + k_db + to_db + nf + loss + range_pwr4_db;
snr = num - den;
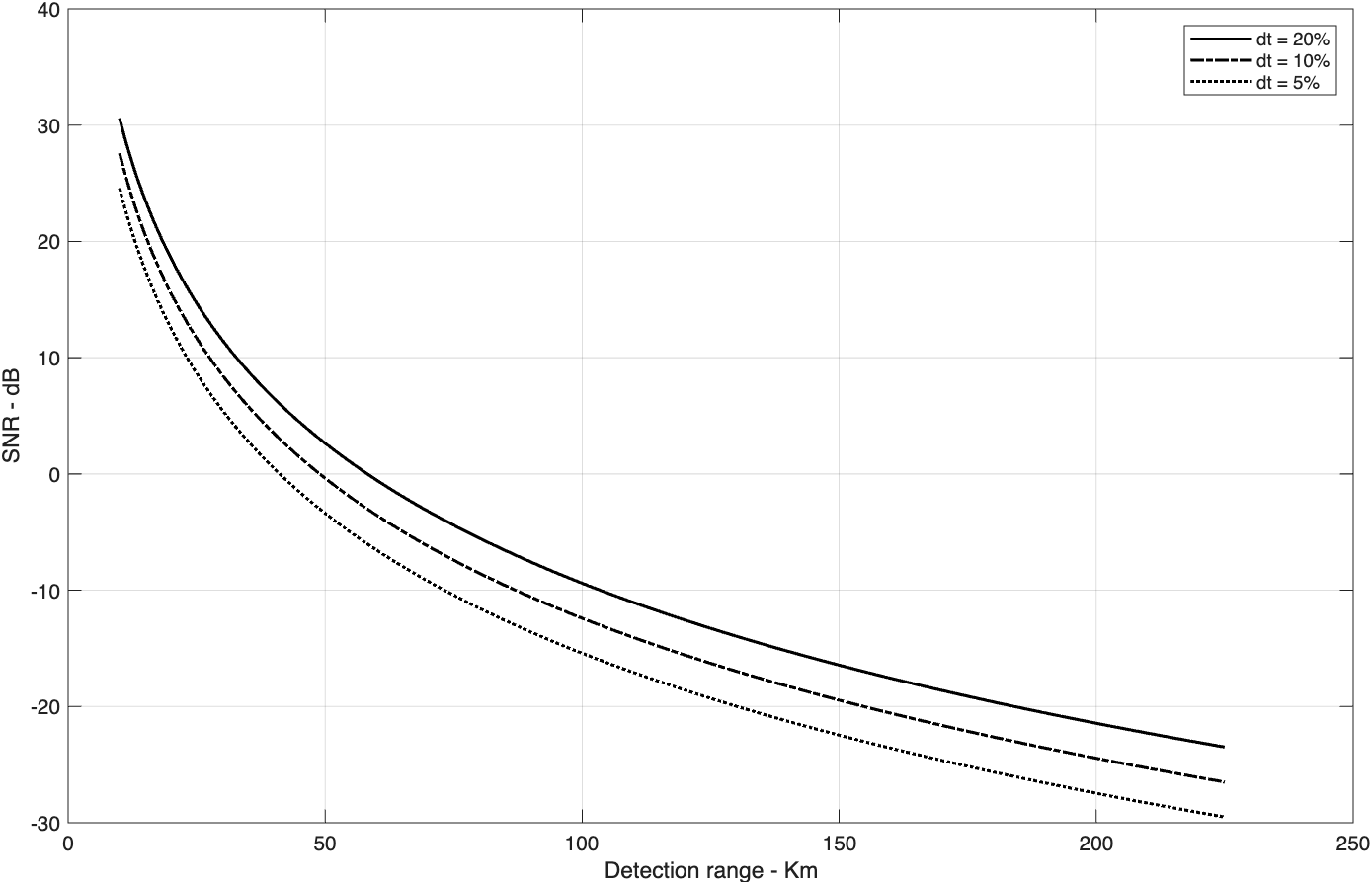
return

函数“hprf_req.m”执行方程（2.30）。语法如下：

[snr]=hprf_req(pt,Ti,g,freq,sigma,dt,range,nf,loss)

SNR=\frac{P_{t}\tau f_rT_iG^2\lambda^2\sigma}{(4\pi)^3R^4kT_0FL}

其中：

符号	说明	单位	状态
pt	峰值功率	W	输入
Ti	目标上的时间	s	输入
g	天线增益	dB	输入
freq	频率	Hz	输入
sigma	目标截面积	m²	输入
dt	占空因子	无	输入
range	目标距离（可以是单值或向量）	km	输入
nf	噪声系数	dB	输入
loss	雷达损耗	dB	输入
snr	SNR（可以是单值或向量）	dB	输出

图2.3给出了函数“hprf_req.m”产生的几种典型输出。

例：

计算一个具有下列参数的高PRF雷达的单个脉冲SNR：峰值功率P_t=100kW，天线增益G=20dB，工作频率f_0=5.6GHz，雷达损耗L=8dB，噪声系数F=5dB，驻留间隔T_i=2s，占空因子dt=0.3。感兴趣的距离R=50km。假设目标的RCS\sigma=0.01m^2。

解：由方程（2.31）得

(SNR)_{dB}=(P_{av}+G^2+\lambda^2+\sigma^2+T_i-(4\pi)^3-R^4-kT_0-F-L)_{dB}

SNR=\frac{P_{av}T_iG^2\lambda^2\sigma}{(4\pi)^3R^4kT_0FL}

下表给出了单位是dB的所有参数：

P_{av}	\lambda^2	T_i	kT_0	(4\pi)^3	R^4	\sigma
44.771	-25.421	3.01	-203.977	32.976	187.959	-20

(SNR)_{dB}=44.771+40-25.421-20+3.01-32.976+203.977-187.959-5-9=12.4dB

通过以下语法采用函数“hprf_req.m”可得到相同的答案：

hprf_req(100e3,2,20,5.6e9,0.01,0.3,50e3,5,8)

MATLAB函数“power_aperture.m”

function PAP = power_aperture(snr,tsc,sigma,range,nf,loss,az_angle,el_angle)
% This function implements Eq. (2.38) of textbook
%
% Inputs:
        % snr       == SNR in dB
        % tsc       == scan time in seconds
        % sigma     == radar cross section in meter squared
        % range     == range to target in Km
        % nf        == noise Figure in dB
        % loss      == total radar losses in dB
        % az_angle  == azimuth search extent in degrees
        % el_angle  == elevation search extent in degrees
%    
% Outputs:
        % PAP       == power aperture product in dB      
% 
Tsc = 10*log10(tsc); % convert Tsc into dB
Sigma = 10*log10(sigma); % convert sigma to dB
four_pi = 10*log10(4.0 * pi); % (4pi) in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
To = 10*log10(290); % noise temp. in dB
range_pwr4_db = 10*log10(range.^4); % target range^4 in dB
omega = (az_angle/57.296) * (el_angle / 57.296); % compute search volume in steraradians
Omega = 10*log10(omega); % search volume in dB
% implement Eq. (1.79)
PAP = snr + four_pi + k_db + To + nf + loss + range_pwr4_db + Omega ...
    - Sigma - Tsc;
return

函数“power_aperture.m”执行方程（2.38）中给出的搜索雷达方程。语法如下：

PAP

SNR=\frac{P_{av}A_e\sigma}{4\pi kT_0FLR^4}\frac{T_{sc}}{\Omega}

其中：

符号	说明	单位	状态
snr	灵敏度	dB	输入
tsc	扫描时间	s	输入
sigma	目标截面积	m²	输入
range	目标距离	km	输入
nf	噪声系数	dB	输入
loss	雷达损耗	dB	输入
az_angle	搜索区域方位上的范围	度	输入
el_angle	搜索区域仰角上的范围	度	输入
PAP	功率孔径积	dB	输出

图2.6给出三种RCS选择的功率孔径积与探测距离的关系曲线图，以及雷达平均功率与功率孔径积的关系曲线图。采用如下的雷达参数：

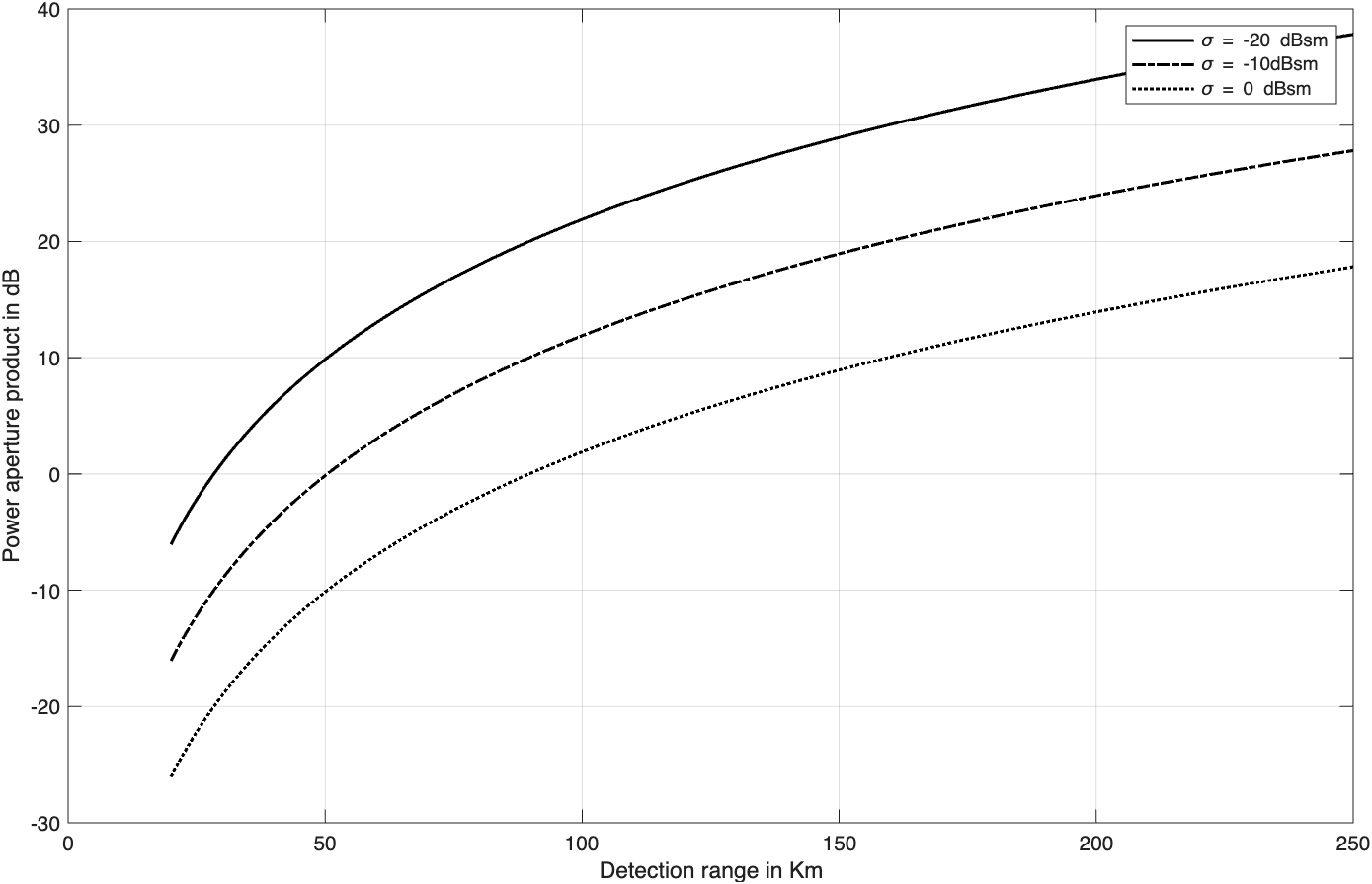
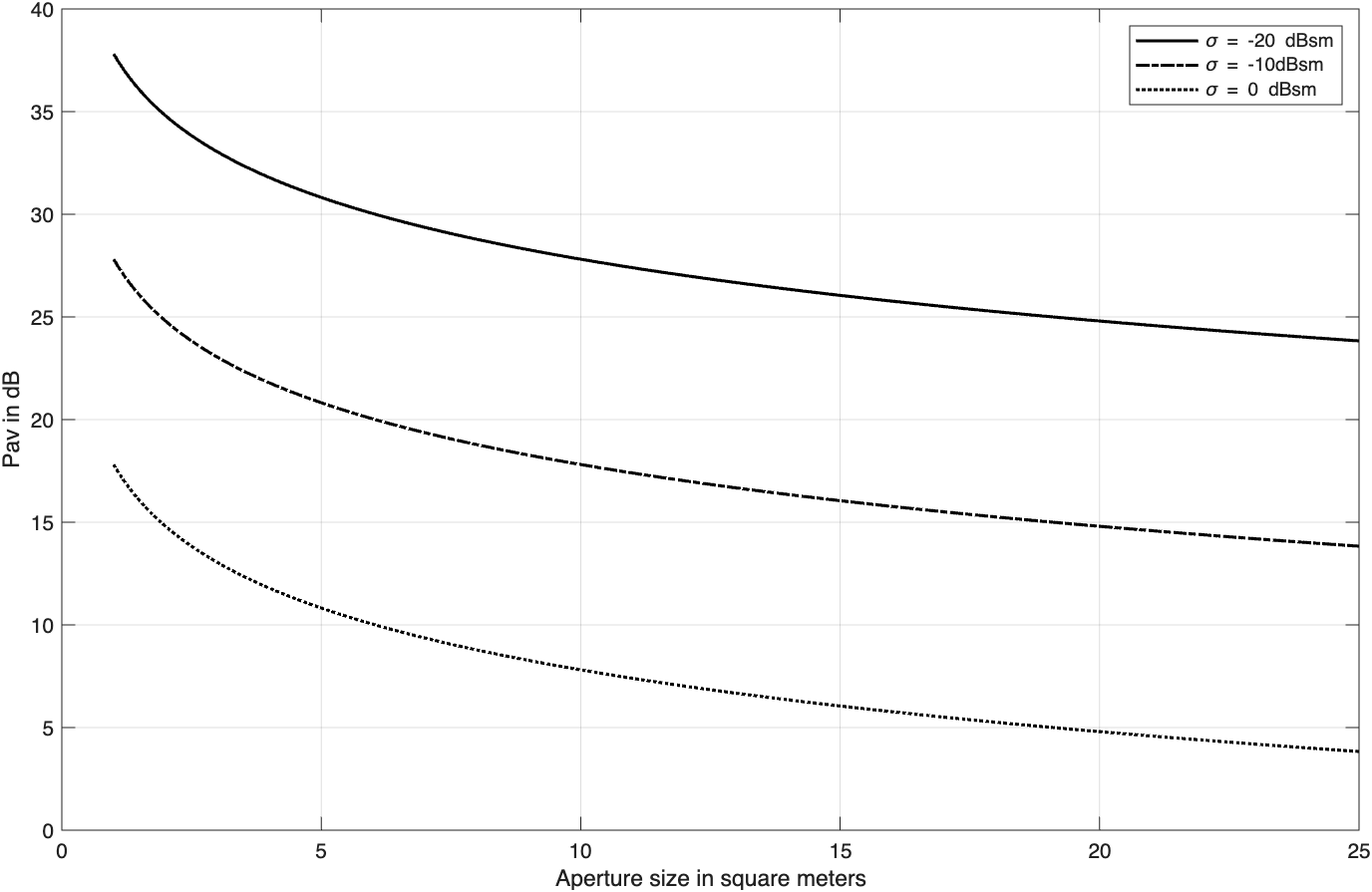
\sigma	T_{sc}	\theta_e=\theta_a	R	nf\times loss	snr
0.1m²	2.5s	2^\circ	250km	13dB	15dB

例：

计算一个具有下列参数的雷达的功率孔径积：扫描时间T_{sc}=2s，噪声系数F=8dB，损耗L=6dB，搜索区域\Omega=7.4sr，感兴趣的距离是R=75km，需要的SNR为20dB。假设\sigma=3.162m^2。

解：注意\Omega=7.4sr对应于四分之三个半球的搜索扇区。因此，使用方程（2.32）得出\theta_a=180^\circ，\theta_e=135^\circ。以如下语法使用MATLAB函数“power_aperture.m”：

PAP=power\_aperture(20,2,3.162,75e3,8,6,180,135)

计算后得到的功率孔径积为36.7dB。

例：

角度覆盖范围在方位角和仰角上都是2^\circ。因此立体角覆盖范围是

\Omega=\frac{2\times2}{(57.23)^2}=-29.132dB

注意，因子360/2\pi=57.23把角度转换为立体角。由方程（2.43）有

(SNR)_{dB}=(P_{av}+A+\sigma+T_{sc}-16-R^4-kT_0-L-F-\Omega)_{dB}

\sigma	T_{sc}	16	R^4	kT_0
-10dB	3.979dB	12.041dB	215.918dB	-203.977dB

由此

15=P_{av}+A-10+3.979-12.041-215.918+203.977-5-8+29.133

那么功率孔径积为

P_{av}+A=38.716dB

现在假设雷达波长\lambda=0.03m，则

A=\frac{G\lambda^2}{4\pi}=3.550dB

P_{av}=-A+38.716=35.166dB

PA{av}=10^{3.5166}=3285.489W

P_t=\frac{P_{av}}{d_t}=\frac{3285.489}{0.3}=10.9512KW

MATLAB函数“ssj_req.m”

function [BR_range] = ssj_req (pt, g, freq, sigma, br, loss, ...
   pj, bj, gj, lossj)
% This function implements Eq.s (2.50) and Eq. (2.52). It also generates
% plot 2.7a
% 
% Inputs
        % pt        == radar peak power in Watts
        % g         == radar antenna gain in dB
        % freq      == radar operating frequency in Hz
        % sigma     == target RCS in squared meters
        % br        == radar bandwidth in Hz
        % loss      == radar losses in dB
        % pj        == jammer power in Watts
        % bj        == jammer bandwidth in Hz
        % gj        == jammer antenna gain in dB
        % loosj     == jammer losses in dB
%
% Outputs
        % BR_range  == cross over range in Km
        
c = 3.0e+8;
lambda = c / freq;
lambda_db = 10*log10(lambda^2);
if (loss == 0.0)
   loss = 0.000001;
end
if (lossj == 0.0)
   lossj =0.000001;
end
sigmadb =10*log10(sigma);
pt_db = 10*log10(pt);
b_db = 10*log10(br);
bj_db = 10*log10(bj);
pj_db = 10*log10(pj);
factor = 10*log10(4.0 *pi);
BR_range = sqrt((pt * (10^(g/10)) * sigma * bj * (10^(lossj/10))) / ...
   (4.0 * pi * pj * (10^(gj/10)) * br * ...
   (10^(loss/10)))) / 1000.0  
s_at_br = pt_db + 2.0 * g + lambda_db + sigmadb - ...
      3.0 * factor - 4.* 10*log10(BR_range) - loss 
index =0;
for ran_var = .1:10:10000
   index = index + 1;
   ran_db = 10*log10(ran_var * 1000.0);
   ssj(index) = pj_db + gj + lambda_db + g + b_db - 2.0 * factor - ...
      2.0 * ran_db - bj_db - lossj + s_at_br ;
   s(index) = pt_db + 2.0 * g + lambda_db + sigmadb - ...
      3.0 * factor - 4.* ran_db - loss + s_at_br ;
end
ranvar = .1:10:10000;
ranvar = ranvar ./ BR_range;
semilogx (ranvar,s,'k',ranvar,ssj,'k-.');
axis([.1 1000 -90 40])
xlabel ('Range normalized to cross-over range');
legend('Target echo','SSJ')
ylabel ('Relative signal or jamming amplitude - dB');
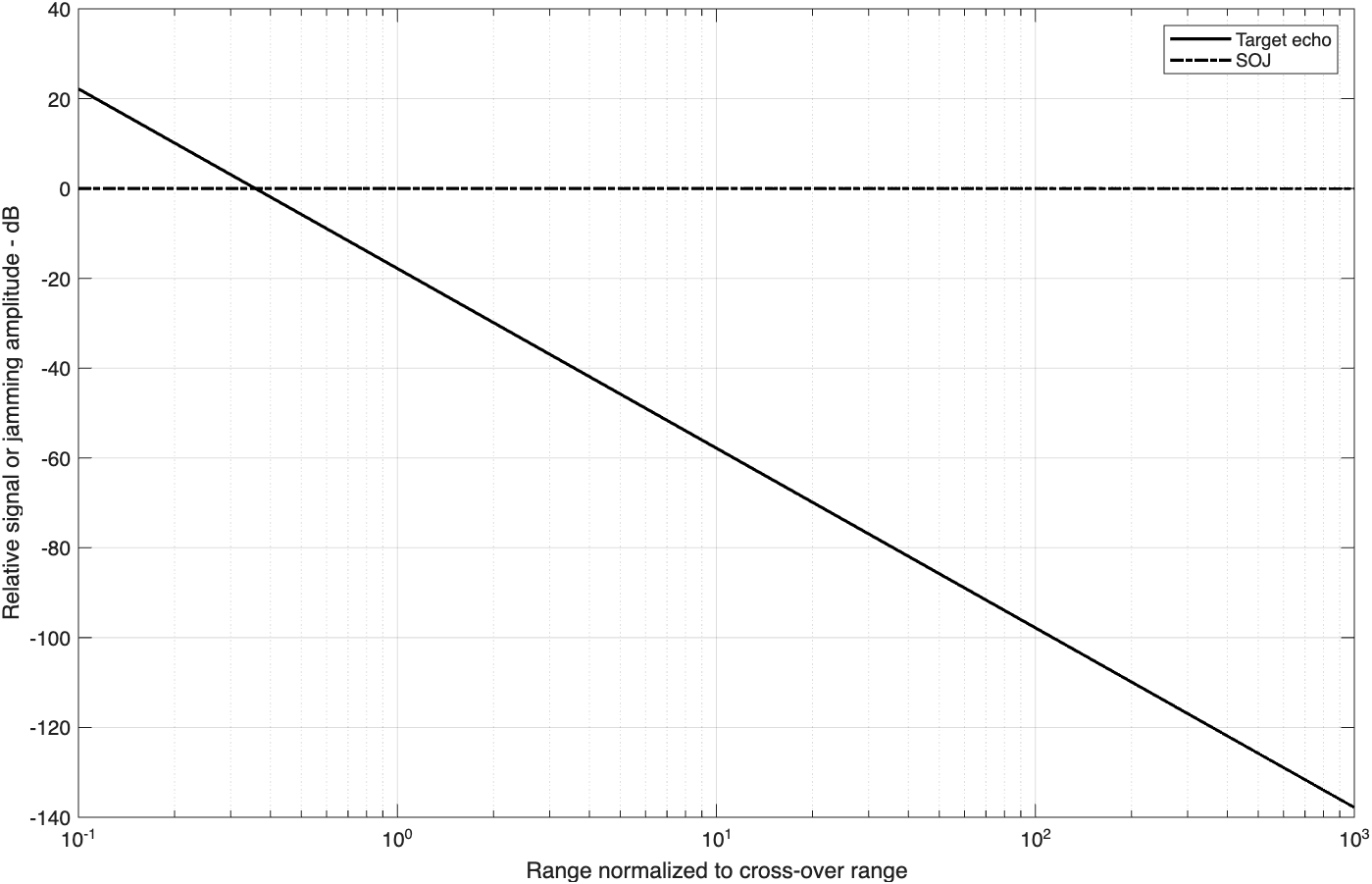
grid

函数“ssj_req.m”执行方程（2.50）和方程（2.52）。语法如下：

[]BR_range=ssj_req(pt,g,freq,sigma,br,loss,pj,bj,gj,lossj)

\frac{S}{J}=\frac{P_t\tau G\sigma B_J}{(ERP)(4\pi)R^2B_rL}
(R_{CO})_{SSJ}=(\frac{P_tG\sigma B_J}{4\pi B_rL(ERP)})^{1/2}

其中：

符号	说明	单位	状态
pt	雷达峰值功率	W	输入
g	雷达天线增益	dB	输入
freq	雷达工作频率	Hz	输入
sigma	目标截面积	m²	输入
br	雷达工作带宽	Hz	输入
loss	雷达损耗	dB	输入
pj	干扰器峰值功率	W	输入
bj	干扰器带宽	Hz	输入
gj	干扰器天线增益	dB	输入
lossj	干扰器损耗	dB	输入
BR_range	跨越距离	km	输出

这个函数生成对跨越距离归一化的相对的S和J与距离的关系图，如图2.7（a）所示。它也计算出跨越距离，如图2.7（b）所示。在这个例子中，使用了下列参数来生成这个图：雷达峰值功率P_t=50kW，干扰器峰值功率P_J=200W，雷达工作带宽B_r=667kHz，干扰器带宽B_J=50MHz，雷达和干扰器损耗为L=L_J=0.10dB，目标截面积\sigma=10m^2，雷达天线增益G=35dB，干扰器天线增益G=35dB，雷达工作频率是f=5.6GHz。

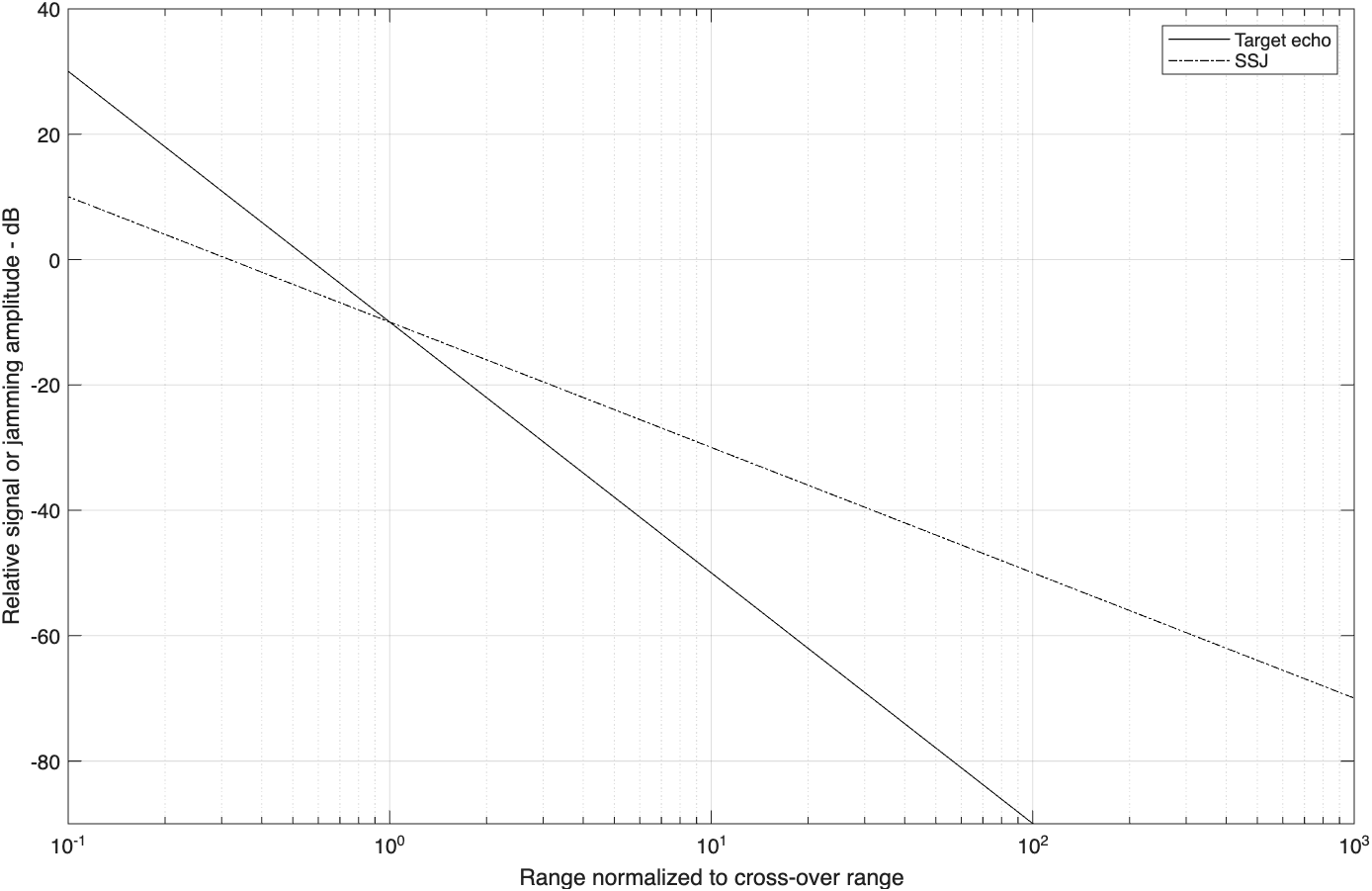
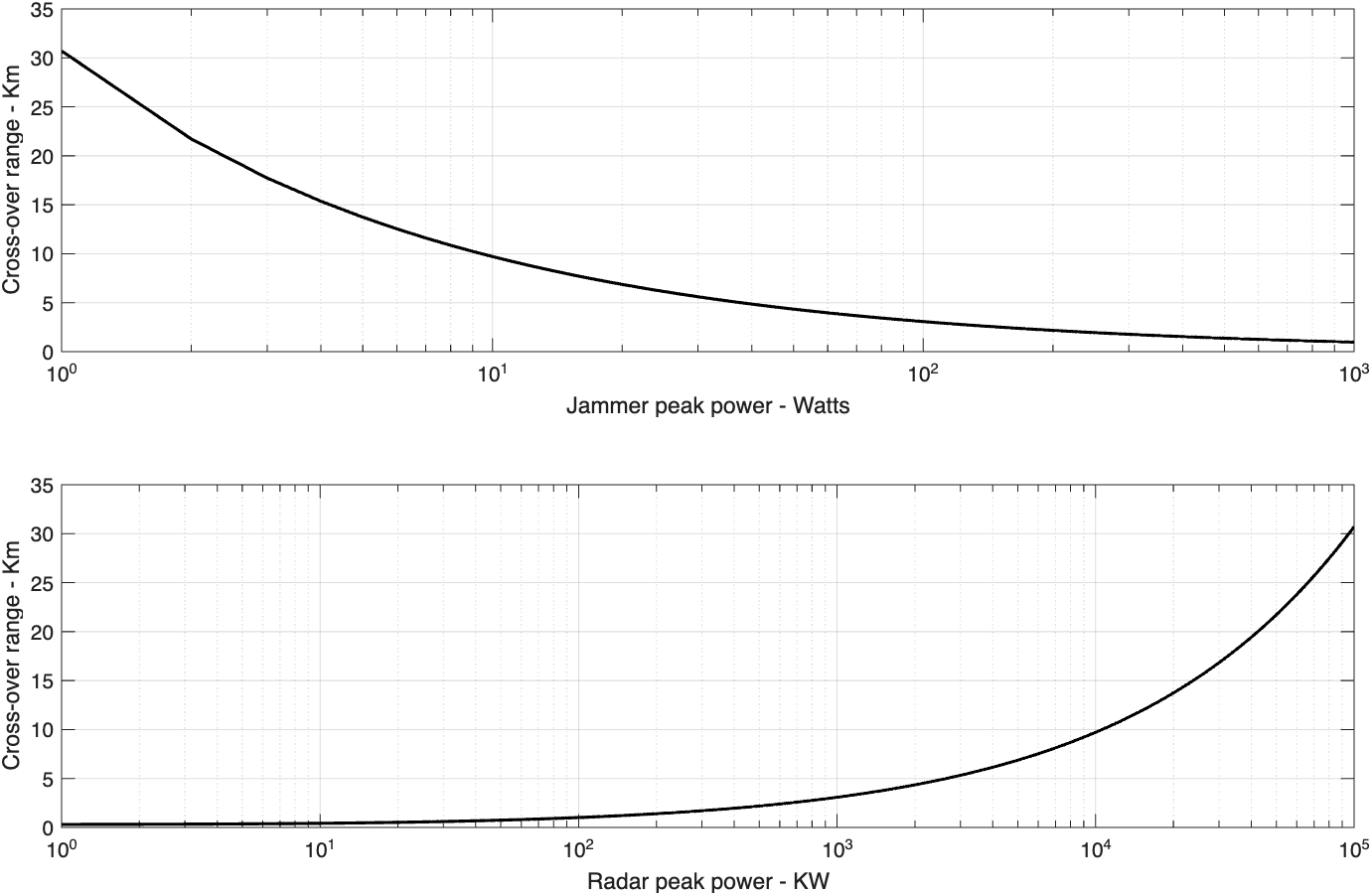
MATLAB函数“sir.m”

function [SIR] = sir (pt, g, sigma, freq, tau, loss, R, pj, bj, gj, lossj);
% This function implements Eq. (2.53) of textbook
% 
% Inputs
        % pt        == radar peak power in Watts
        % g         == radar antenna gain in dB
        % freq      == radar operating frequency in Hz
        % tau       == radar pulse width in seconds
        % loss      == radar losses in dB
        % R         == target range in Km, can be single value or vector
        % pj        == jammer power in Watts
        % bj        == jammer bandwidth in Hz
        % gj        == jammer antenna gain in dB
        % loosj     == jammer losses in dB
%
% Outputs
        % SIR  == S/(J+N) in dB
c = 3.0e+8;
k = 1.38e-23;
%R = linspace(rmin, rmax, 1000);
range = R .* 1000;
lambda = c / freq;
gj = 10^(gj/10);
G = 10^(g/10);
ERP1 = pj * gj / lossj;
ERP_db = 10*log10(ERP1);
Ar = lambda *lambda * G / 4 /pi;
num1 = pt * tau * G * sigma * Ar;
demo1 = 4^2 * pi^2 * loss .* range.^4;
demo2 = 4 * pi * bj .* range.^2;
num2 = ERP1 * Ar;
val11 = num1 ./ demo1;
val21 = num2 ./demo2; 
sir = val11 ./ (val21 + k * 290);
SIR = 10*log10(sir);
end

MATLAB函数“sir.m”执行方程（2.53），其语法如下：

[SIR]=sir(pt,g,sigma,freq,tau,loss,R,pj,bj,gj,lossj)

其中：

符号	说明	单位	状态	值
pt	雷达峰值功率	W	输入	50kW
g	雷达天线增益	dB	输入	35dB
sigma	目标截面积	m²	输入	10m²
freq	雷达工作频率	Hz	输入	5.6GHz
tau	雷达脉冲宽度	s	输入	50ms
loss	雷达损耗	dB	输入	5dB
R	距离（可以是单值或向量）	km	输入	linspace（10 400 5000）km
pj	干扰器峰值频率	W	输入	200W
bj	干扰器带宽	Hz	输入	50MHz
gj	干扰器天线增益	dB	输入	10dB
lossj	干扰器损耗	dB	输入	0.3dB
SIR	S/(J+N)	dB	输出

\frac{S}{J+N}=\frac{(P_tG\sigma A_r\tau)/((4\pi)^2R^4L)}{(\frac{(ERP)A_r}{4\pi R^2B_J}+kT_0)}

这个函数“sir.m”产生的数据可以用来绘制S/(J+N)和探测距离的曲线，如图2.8所示，输入上表中定义的参数。

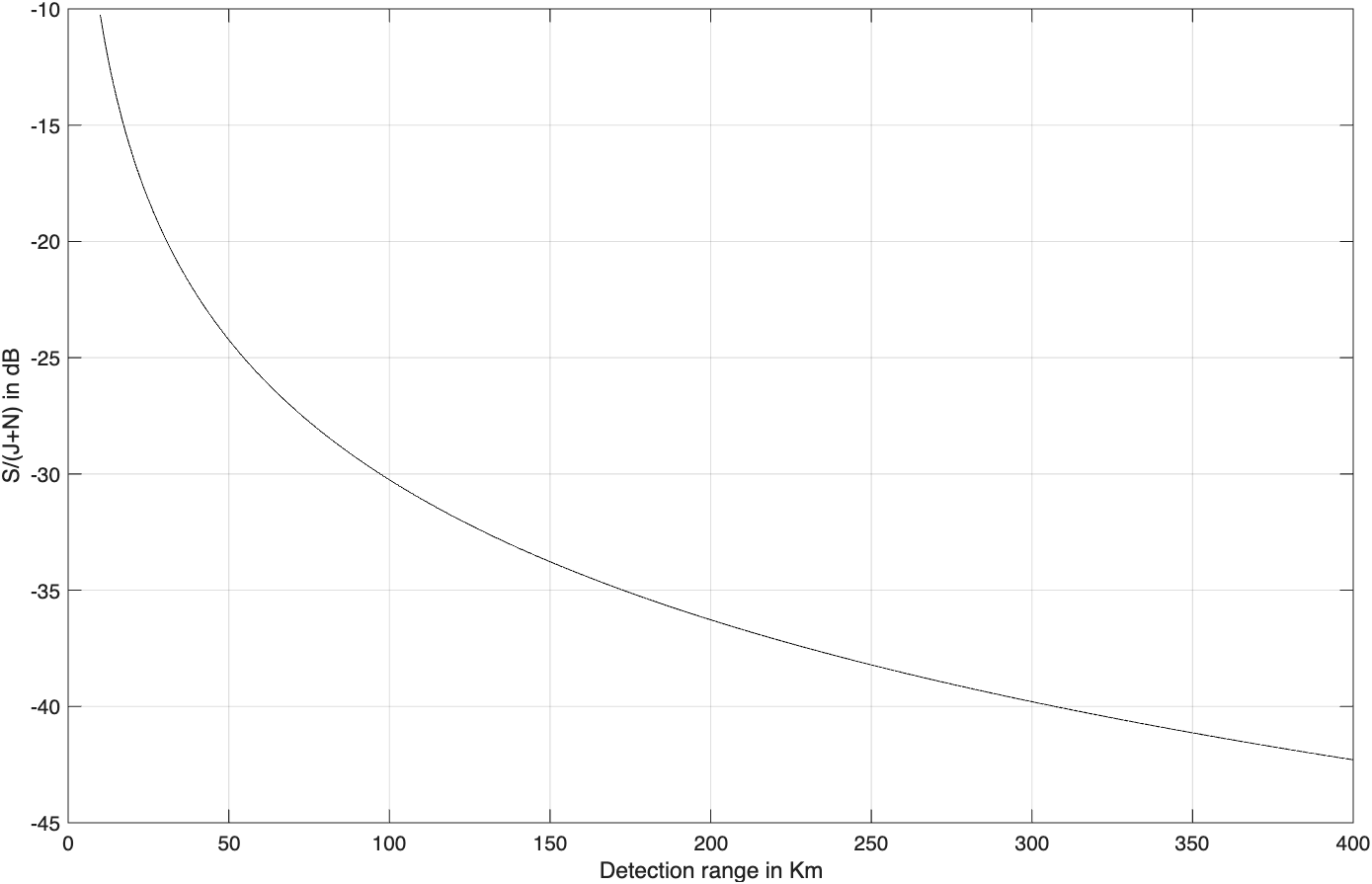
MATLAB函数“burn_thru.m”

function [Range] = burn_thru (pt, g, sigma, freq, tau, loss, pj, bj, gj, lossj,sir0,ERP);
% This function implements Eq. (254) of textbook
% 
% Inputs
        % pt        == radar peak power in Watts
        % g         == radar antenna gain in dB
        % freq      == radar operating frequency in Hz
        % tau       == radar pulse width in seconds
        % loss      == radar losses in dB
        % pj        == jammer power in Watts
        % bj        == jammer bandwidth in Hz
        % gj        == jammer antenna gain in dB
        % loosj     == jammer losses in dB
        % sir0      == desired SIR in dB
        % ERP       == desired jammer ERP, single value or vector in Watts
%
% Outputs
        % Range  == burn through range in Km
c = 3.0e+8;
k = 1.38e-23;
sir0 = 10^(sir0/10);
lambda = c / freq;
gj = 10^(gj/10);
G = 10^(g/10);
Ar = lambda *lambda * G / 4 /pi;
num32 = ERP .* Ar;
demo3 = 8 *pi * bj * k * 290;
demo4 = 4^2 * pi^2 * k * 290 * sir0;
val1 = (num32 ./ demo3).^2;
val2 = (pt * tau * G * sigma * Ar)/(4^2 * pi^2 * loss * sir0 * k * 290);
val3 = sqrt(val1 + val2);
val4 = (ERP .* Ar) ./ demo3;
Range = sqrt(val3 - val4) ./ 1000;
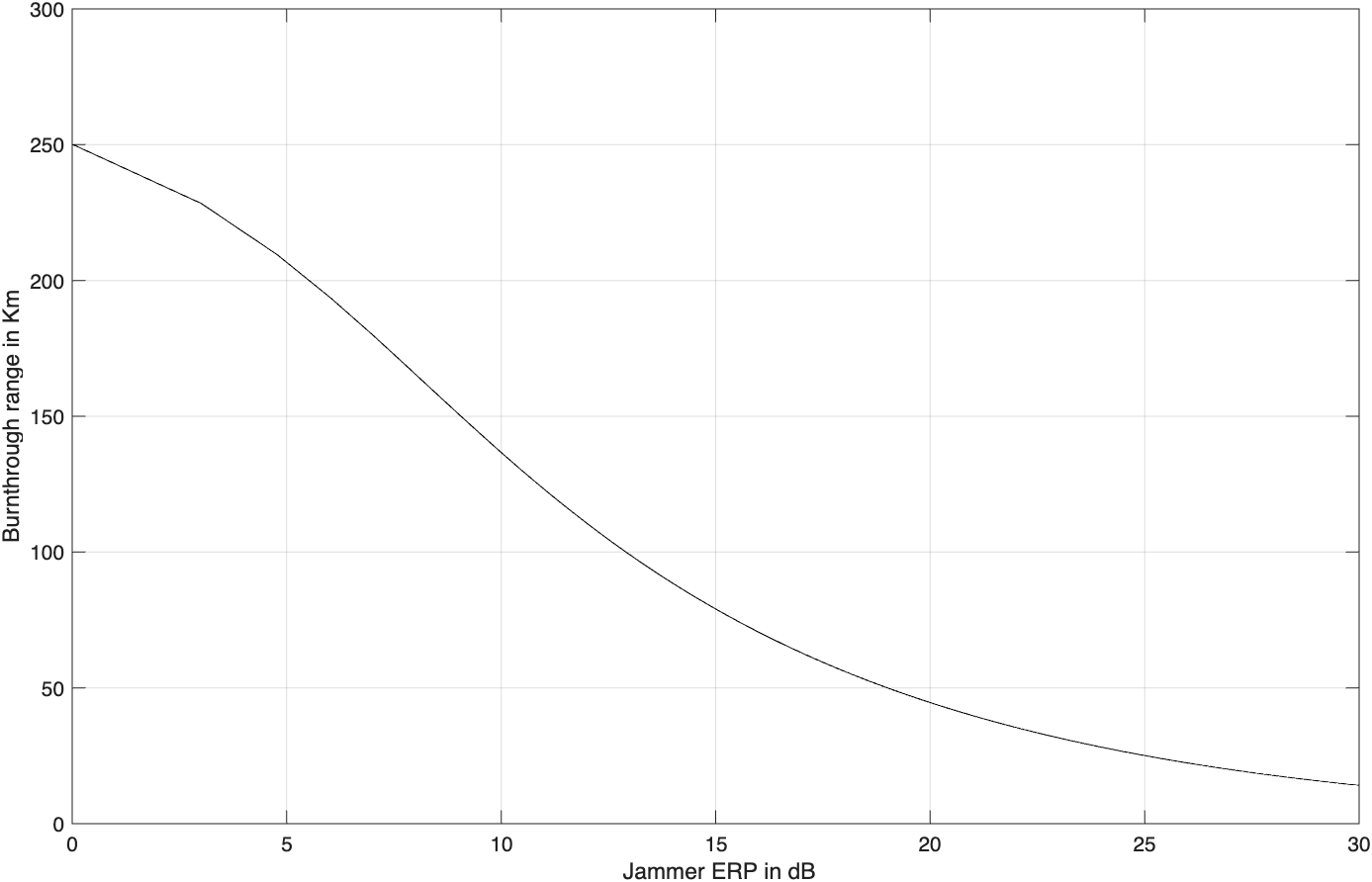
end

MATLAB函数“burn_thru.m”执行方程（2.54）。它产生S/(J+N)与探测距离的关系曲线及烧穿距离与干扰器ERP的关系曲线。语法如下：

[Range]=burn_thru(pt,g,sigma,freq,tau,loss,pj,bj,gj,lossj,sir0,ERP)

其中：

符号	说明	单位	状态	值
pt	雷达峰值功率	W	输入	50kW
g	雷达天线增益	dB	输入	35dB
sigma	目标截面积	m²	输入	10m²
freq	雷达工作频率	Hz	输入	5.6GHz
tau	雷达脉冲宽度	s	输入	0.5ms
loss	雷达损耗	dB	输入	5dB
pj	干扰器峰值频率	W	输入	200W
bj	干扰器带宽	Hz	输入	500MHz
gj	干扰器天线增益	dB	输入	10dB
lossj	干扰器损耗	dB	输入	0.3dB
sir0	需要的SIR	dB	输入	15dB
ERP	需要的ERP，可以是向量	W	输入	linspace（1 1000 1000）W
Range	烧穿距离	km	输出

R_{BT}=\{\sqrt{(\frac{(ERP)A_r}{8\pi B_JkT_0})^2+\frac{P_tG\sigma A_r\tau}{(4\pi)^2L\frac{S}{J+N}kT_0}}-\frac{(ERP)A_r}{8\pi B_JkT_0}\}^{\frac{1}{2}}

MATLAB函数"soj_req.m"

function [BR_range] = soj_req (pt, g, sigma, b, freq, loss, range, ...
   pj, bj,gj, lossj, gprime, rangej)
% This function implements Eqs. (257) and (2.58) of textbook
%
% Inputs
        % pt        == radar peak power in Watts
        % g         == radar antenna gain in dB
        % sigma     == target RCS in sdBsm 
        % freq      == radar operating frequency in Hz
        % tau       == radar pulse width in seconds
        % loss      == radar losses in dB
        % range     == range to target in Km
        % pj        == jammer power in Watts
        % bj        == jammer bandwidth in Hz
        % gj        == jammer antenna gain in dB
        % loosj     == jammer losses in dB
        % gprime    == jammer antenna gain
        % rangej    == range to jammer in Km
%
% Outputs
        % BR_Range  == burn through range in Km
%
c = 3.0e+8;
lambda = c / freq;
lambda_db = 10*log10(lambda^2);
if (loss == 0.0)
   loss = 0.000001;
end
if (lossj == 0.0)
   lossj =0.000001;
end
sigmadb = 10*log10(sigma);
range_db = 10*log10(range * 1000.);
rangej_db = 10*log10(rangej * 1000.);
pt_db = 10*log10(pt);
b_db = 10*log10(b);
bj_db = 10*log10(bj);
pj_db = 10*log10(pj);
factor = 10*log10(4.0 *pi);
BR_range = ((pt * 10^(2.0*g/10) * sigma * bj * 10^(lossj/10) * ...
   (rangej)^2) / (4.0 * pi * pj * 10^(gj/10) * 10^(gprime/10) * ...
   b * 10^(loss/10)))^.25 / 1000. 
end

函数"soj_req.m"执行方程（2.57）和方程（2.58）。函数"soj_req.m"的输入内容与SSJ情况的输入相同，但是还有两项额外的输入：干扰器方向上的雷达天线增益G'和雷达到干扰器的距离R_J。语法如下：

[BR_range]soj_req(pt,g,sigma,b,freq,loss,range,pj,bj,gj,lossj,gprime,rangej)

\frac{S}{J}=\frac{P_tG^2R_J^2\sigma B_JG_{PC}}{4\pi(ERP)G'R^4B_rL}

图2.10是使用这个函数产生的图形。在这种情况下，使用与SSJ情况下相同的参数，干扰器峰值功率P_J=5000W，干扰器天线增益G_J=30dB，干扰器方向上的雷达天线增益G_J=30dB，雷达到干扰器的距离R_J=22.2km。如果干扰采用高斯噪声的形式，雷达接收机必须以处理雷达内部噪声功率的相同方式来处理干扰信号。在这种情况下，S/(J+N)为

\frac{S}{J+N}=\frac{(\frac{P_tG\sigma A_r\tau}{(4\pi)^2R^4L})}{(\frac{(ERP)A_rG'}{4\pi R^2B_J}+kT_0)}

MATLAB函数“range_calc.m”

function [output_par] = range_calc (pt, tau, fr, time_ti, gt, gr, freq, ...
   sigma, te, nf, loss, snro, pcw, range, radar_type, out_option)
c = 3.0e+8;
lambda = c / freq;
if (radar_type == 0)
   pav = pcw;
else
   % Compute the duty cycle
   dt = tau * 0.001 * fr;
   pav = pt * dt;
end
pav_db = 10.0 * log10(pav);
   lambda_sqdb = 10.0 * log10(lambda^2);
   sigmadb = 10.0 * log10(sigma);
   for_pi_cub = 10.0 * log10((4.0 * pi)^3);
   k_db = 10.0 * log10(1.38e-23);
   te_db = 10.0 * log10(te);
   ti_db = 10.0 * log10(time_ti);
   range_db = 10.0 * log10(range * 1000.0);
if (out_option == 0)
   %compute SNR
      % Implement Eq. (3.63)
   snr_out = pav_db + gt + gr + lambda_sqdb + sigmadb + ti_db - ...
      for_pi_cub - k_db - te_db - nf - loss - 4.0 * range_db
   index = 0;
   for range_var = 10:10:1000
      index = index + 1;
      rangevar_db = 10.0 * log10(range_var * 1000.0);
      snr(index) = pav_db + gt + gr + lambda_sqdb + sigmadb + ti_db - ...
         for_pi_cub - k_db - te_db - nf - loss - 4.0 * rangevar_db;
   end
   var = 10:10:1000;
   plot(var,snr,'k')
   xlabel ('Range - Km');
   ylabel ('SNR - dB');
   grid
else
  range4 = pav_db + gt + gr + lambda_sqdb + sigmadb + ti_db - ...
     for_pi_cub - k_db - te_db - nf - loss - snro;
  range = 10.0^(range4/40.) / 1000.0
   index = 0;
  for snr_var = -20:1:60
     index = index + 1;
     rangedb = pav_db + gt + gr + lambda_sqdb + sigmadb + ti_db - ...
        for_pi_cub - k_db - te_db - nf - loss - snr_var;
     range(index) = 10.0^(rangedb/40.) / 1000.0;
  end
  var = -20:1:60;
  plot(var,range,'k')
  xlabel ('Minimum SNR required for detection - dB');
  ylabel ('Maximum detection range - Km');
  grid
end
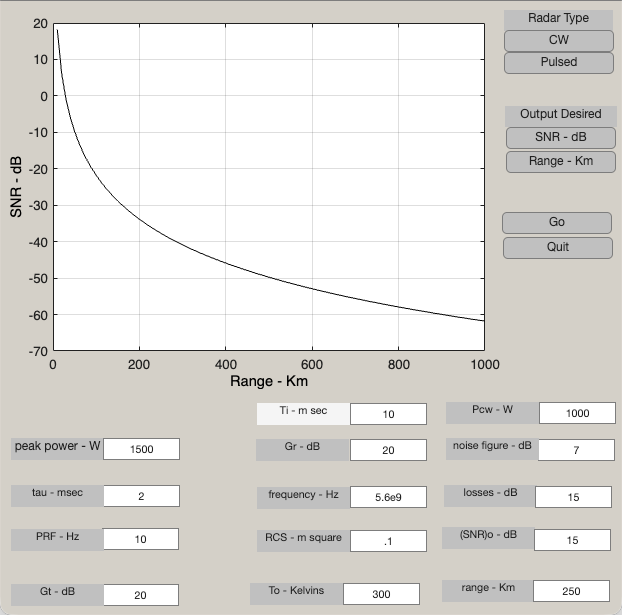
return

程序“range_calc.m”求解以下形式的雷达距离方程：

R=(\frac{P_t\tau f_rT_iG_tG_r\lambda^2\sigma}{(4\pi)^3kT_0FL(SNR)_o})^{\frac{1}{4}}

式中，P_t为发射峰值功率，\tau为脉冲宽度，f_r为PRF，G_t和G_r分别为发射和接收天线增益，\lambda为波长，\sigma为目标截面积，k为玻尔兹曼常数，T_0为290K，F为系统噪声系统，L为整个系统的损耗，并且(SNR)_o为探测所需的最小SNR。

可以选择连续波或脉冲雷达。在连续波雷达的情况下，在代码中P_t\tau f_r项用平均连续波功率P_{CW}代替。另外，T_i项指驻留间隔。而在脉冲雷达的情况下，T_i表示在目标上的时间。图2.25的曲线用图中所示参数描绘了脉冲雷达SNR与探测距离关系的一个例子。在输入和编辑所有输入参数时，使用了一个基于MATLAB的图形用户界面（GUI）。输出包括最大探测距离与最小SNR关系的图形。

三、线性系统与复信号表示法

线性调频（LFM）信号

调频或调相信号可用来实现更宽的工作带宽。线性调频（LFM）信号广泛用于大多数现代雷达系统。在此情况下，频率线性地向上（上线性调频）或向下（下线性调频）扫过脉冲宽度。图3.6显示了一个典型的线性调频波形的例子。脉冲宽度为\tau_0，带宽为B。

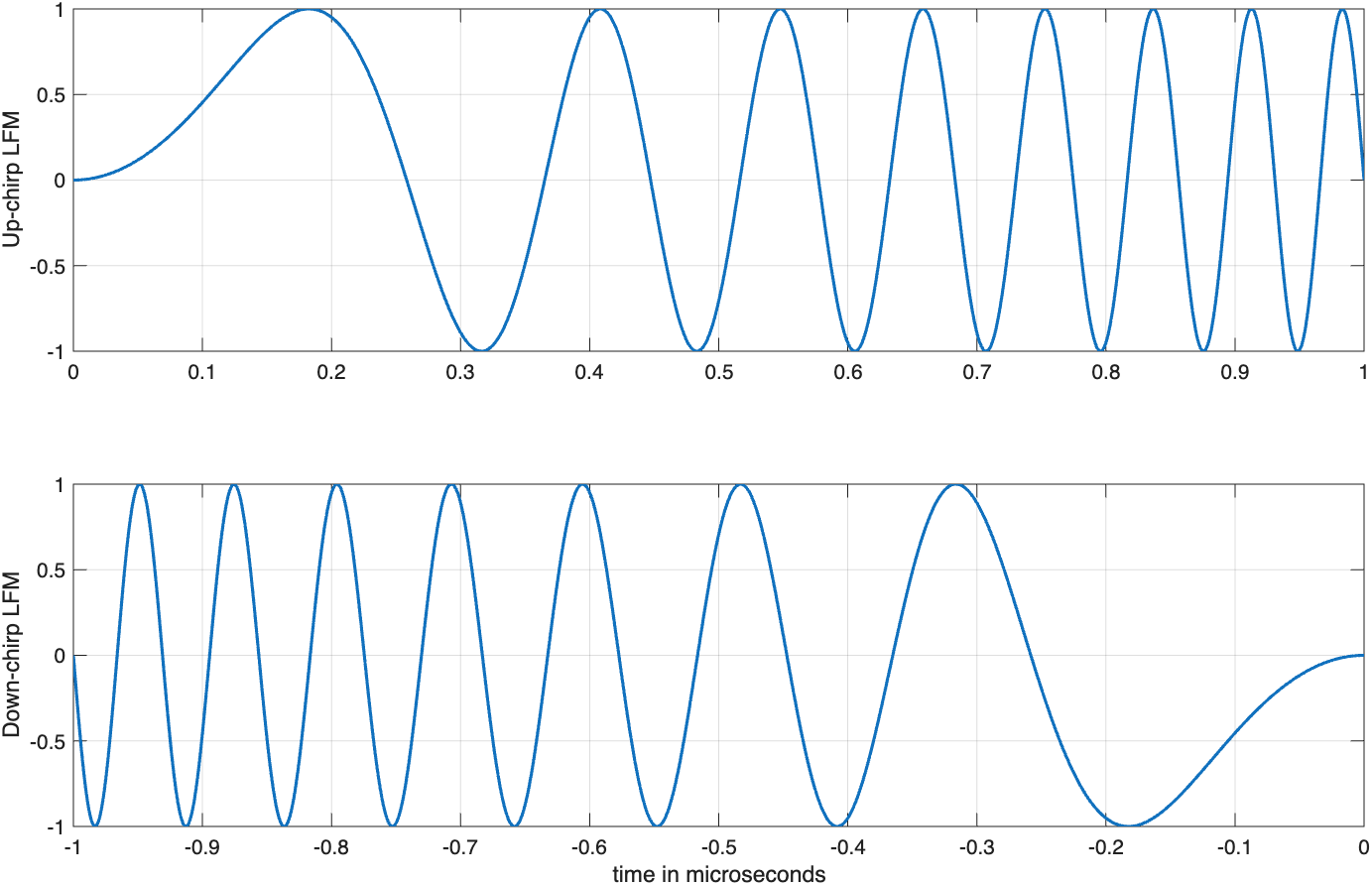
向上线性调频瞬时相位可表示为

\phi(t)=2\pi(f_0t+\frac{\mu}{2}t^2)\text{ }-\frac{\tau_0}{2}\le t\le\frac{\tau_0}{2}

式中，f_0为雷达中心频率，\mu=B/\tau_0是线性调频系数。因此，瞬时频率为

f(t)=\frac{1}{2\pi}\frac{d}{dt}\phi(t)=f_0+\mu t\text{ }-\frac{\tau_0}{2}\le t\le\frac{\tau_0}{2}

类似地，向下线性调频瞬时相位和频率分别为

\phi(t)=2\pi(f_0t-\frac{\mu}{2}t^2)\text{ }-\frac{\tau_0}{2}\le t\le\frac{\tau_0}{2}

f(t)=\frac{1}{2\pi}\frac{d}{dt}\phi(t)=f_0-\mu t\text{ }-\frac{\tau_0}{2}\le t\le\frac{\tau_0}{2}

典型线性调频波形可表示为

x_1(t)=Rect(\frac{t}{\tau_0})e^{j2\pi(f_0t+\frac{\mu}{2}t^2)}

式中，Rect(t/\tau_0)表示宽度为\tau_0的矩形脉冲。记住，信号x_1(t)是线性调频波形的解析信号。由此可得

x_1(t)=\tilde{x}(t)e^{j2\pi f_0t}

\tilde{x}(t)=Rect(\frac{t}{\tau_0}e^{j\pi \mu t^2})

信号x_1(t)的谱由其复包络\tilde{x}(t)确定。方程（3.114）中的复指数项引入了一个关于中心频率f_0的频移。求\tilde{x}(t)的傅立叶变换得到

\tilde{X}(f)=\int^\infty_{-\infty}Rect(\frac{t}{\tau_0})e^{j\pi\mu t^2}e^{-j2\pi ft}dt=\int^{\frac{\tau_0}{2}}_{-\frac{\tau_0}{2}}e^{-j2\pi ft}dt

设\mu'=\pi \mu=\pi B/\tau_0，并进行变量变换

(z=\sqrt{\frac{2}{\pi}}(\sqrt{\mu'}-\frac{\pi f}{\sqrt{\mu'}}));\sqrt{\frac{\pi}{2\mu'}}\text{ }dz=dt

于是，方程（3.115）可写成

\tilde{X}(f)=\sqrt{\frac{\pi}{2\mu'}}e^{-j(\pi f)^2/\mu'}\int^{z_2}_{-z_1}e^{j\pi z^2/2}dz

\tilde{X}(f)=\sqrt{\frac{\pi}{2\mu'}}e^{-j(\pi f)^2/\mu'}\{\int^{z_2}_0e^{j\pi z^2/2}dz-\int^{-z_1}_0e^{j\pi z^2/2}dz\}

z_1=-\sqrt{\frac{2\mu'}{\pi}}(\frac{\tau_0}{2}+\frac{\pi f}{\mu'})=\sqrt{\frac{B\tau_0}{2}}(1+\frac{f}{B/2})

z_2=\sqrt{\frac{\mu'}{\pi}}(\frac{\tau_0}{2}-\frac{\omega}{\mu'})=\sqrt{\frac{B\tau_0}{2}}(1-\frac{f}{B/2})

用C(z)和S(z)表示菲涅耳（Fresnel）积分，定义为

C(z)=\int^z_0\cos{\frac{\pi v^2}{2}}dv\text{ }S(z)=\int^z_0\sin{\frac{\pi v^2}{2}}dv

菲涅耳积分可近似表示为

C(z)\approx\frac{1}{2}+\frac{1}{\pi z}\sin{(\frac{\pi}{2}z^2)};z\ge1

S(z)\approx\frac{1}{2}-\frac{1}{\pi z}\cos{(\frac{\pi}{2}z^2)};z\ge1

注意，C(-z)=-C(z)，S(-z)=-S(z)。图3.7显示了当0\le z\le4.0时C(z)和S(z)的图形。将方程（3.121）代入方程（3.118）并进行积分得到

\tilde{X}(f)=\sqrt{\frac{\pi}{2\mu'}}e^{-j(\pi f)^2/(\mu')}\{[C(z_2)+C(z_1)]+j[S(z_2)+S(z_1)]\}

图3.8显示了线性调频波形实部、虚部和幅度谱的典型曲线。图3.8（c）给出的方形谱是众所周知的菲涅耳谱。

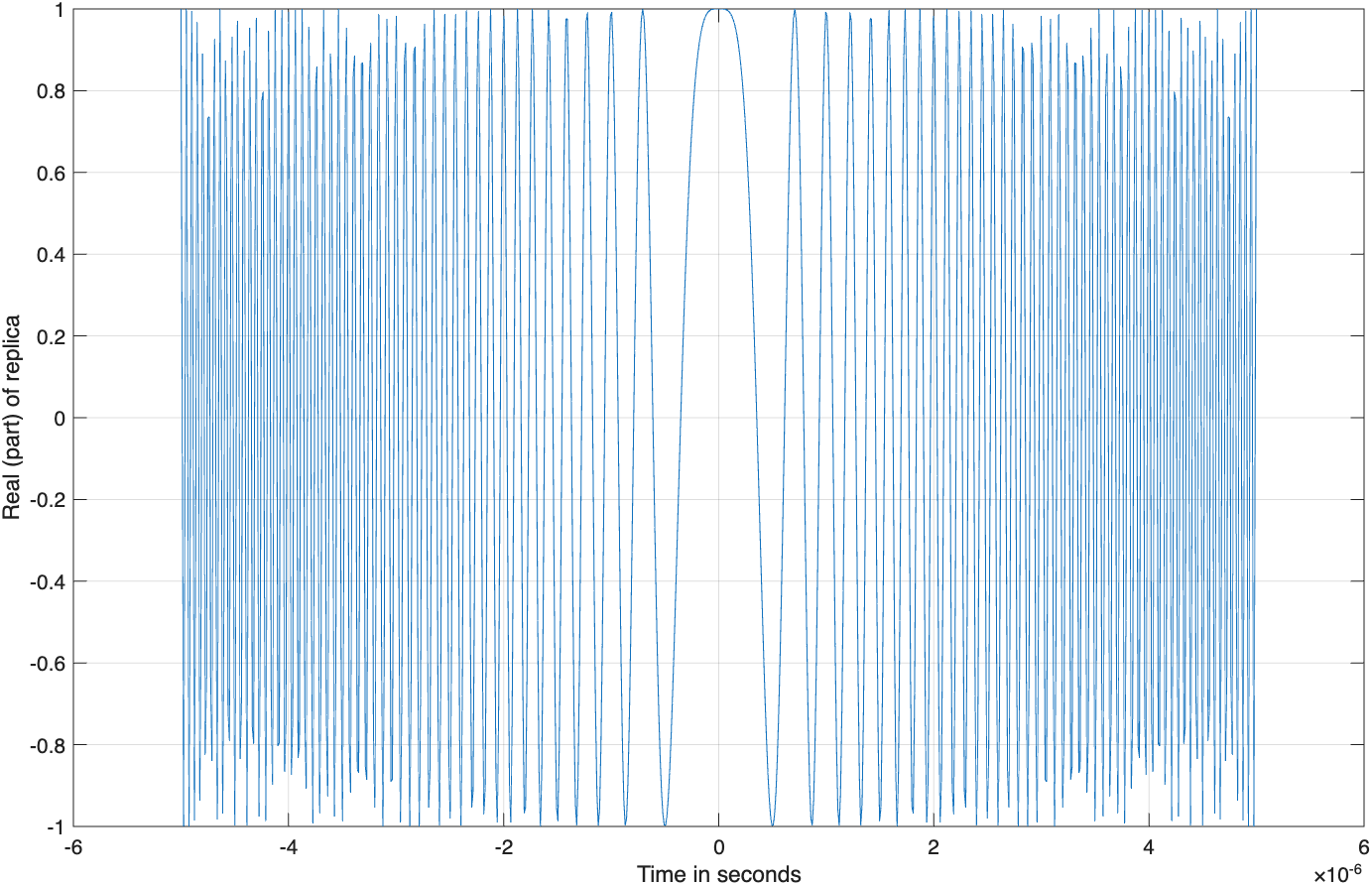
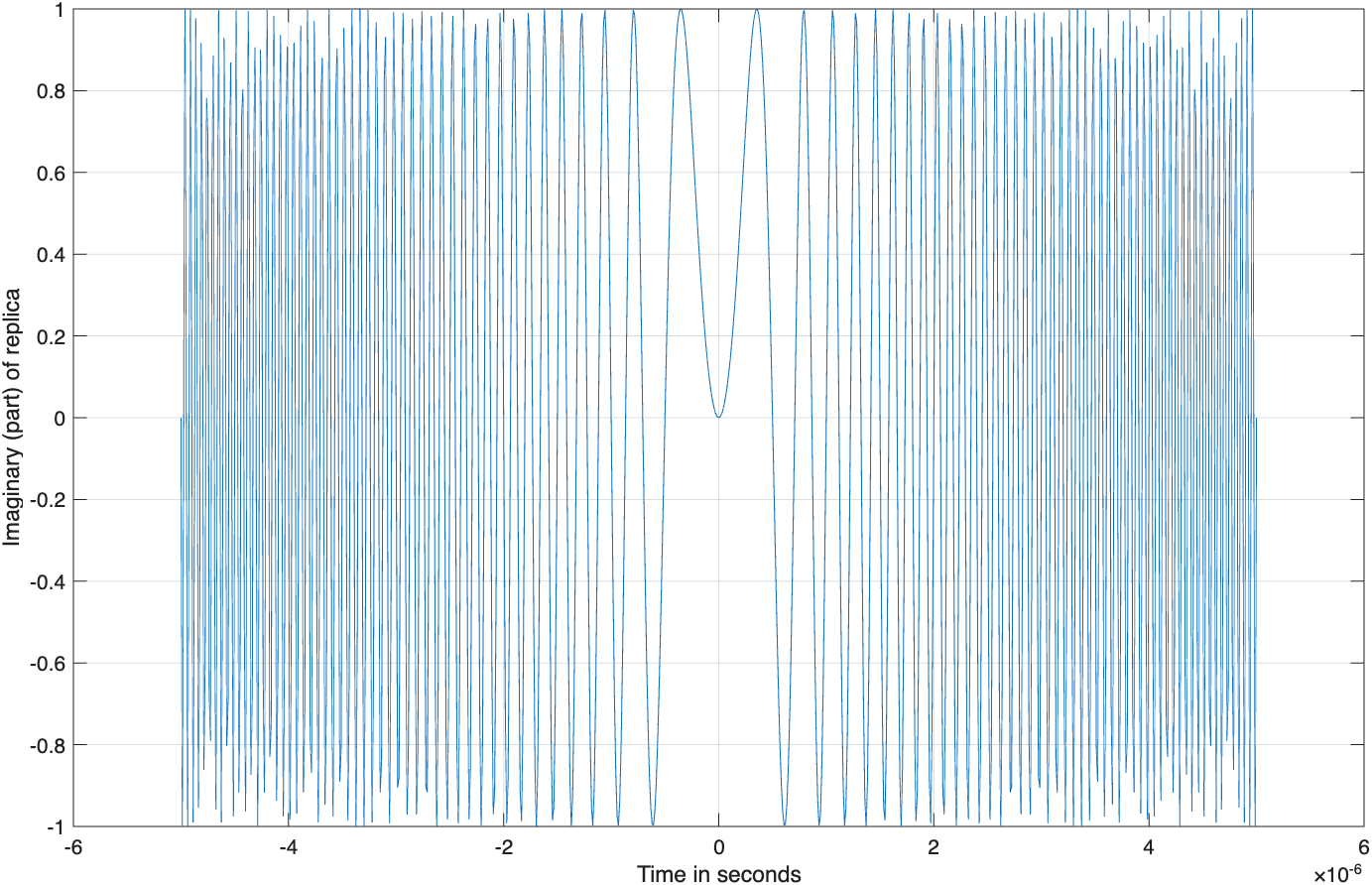
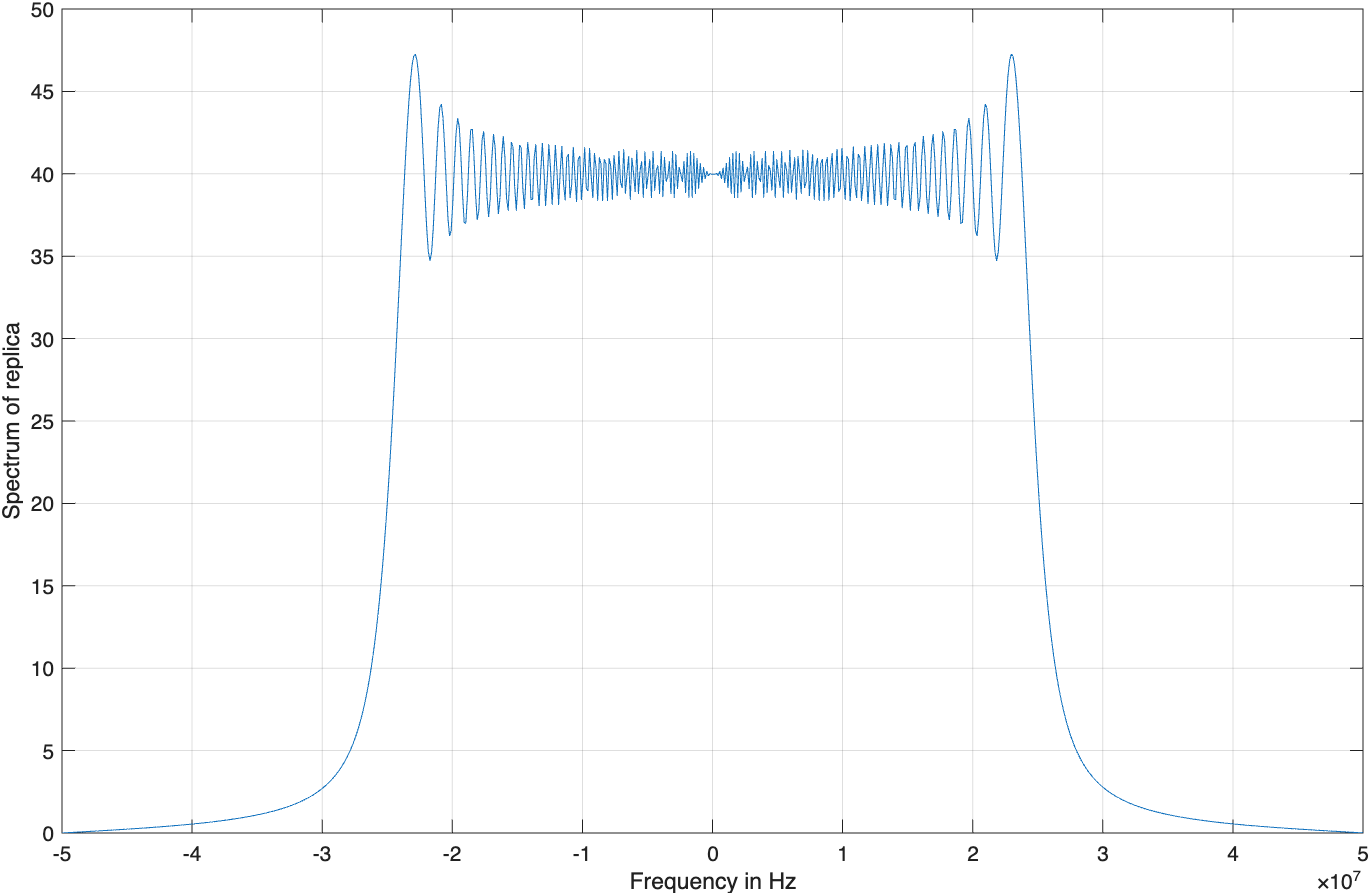
加窗技术

序列x(n)的截短可通过计算下面的乘积来实现：

x_w(n)=x(n)w(n)

式中，

w(n)=\begin{cases} f(n);n=0,1,...,N-1\\ 0\text{ 其他} \end{cases}

其中，f(n)\le1。有限序列w(n)称为加窗序列，或者简称为窗。加窗过程应不影响截短序列的相位响应，因此序列w(n)必须保持线性相位。这可以通过使窗函数相对于其中心点对称来实现。

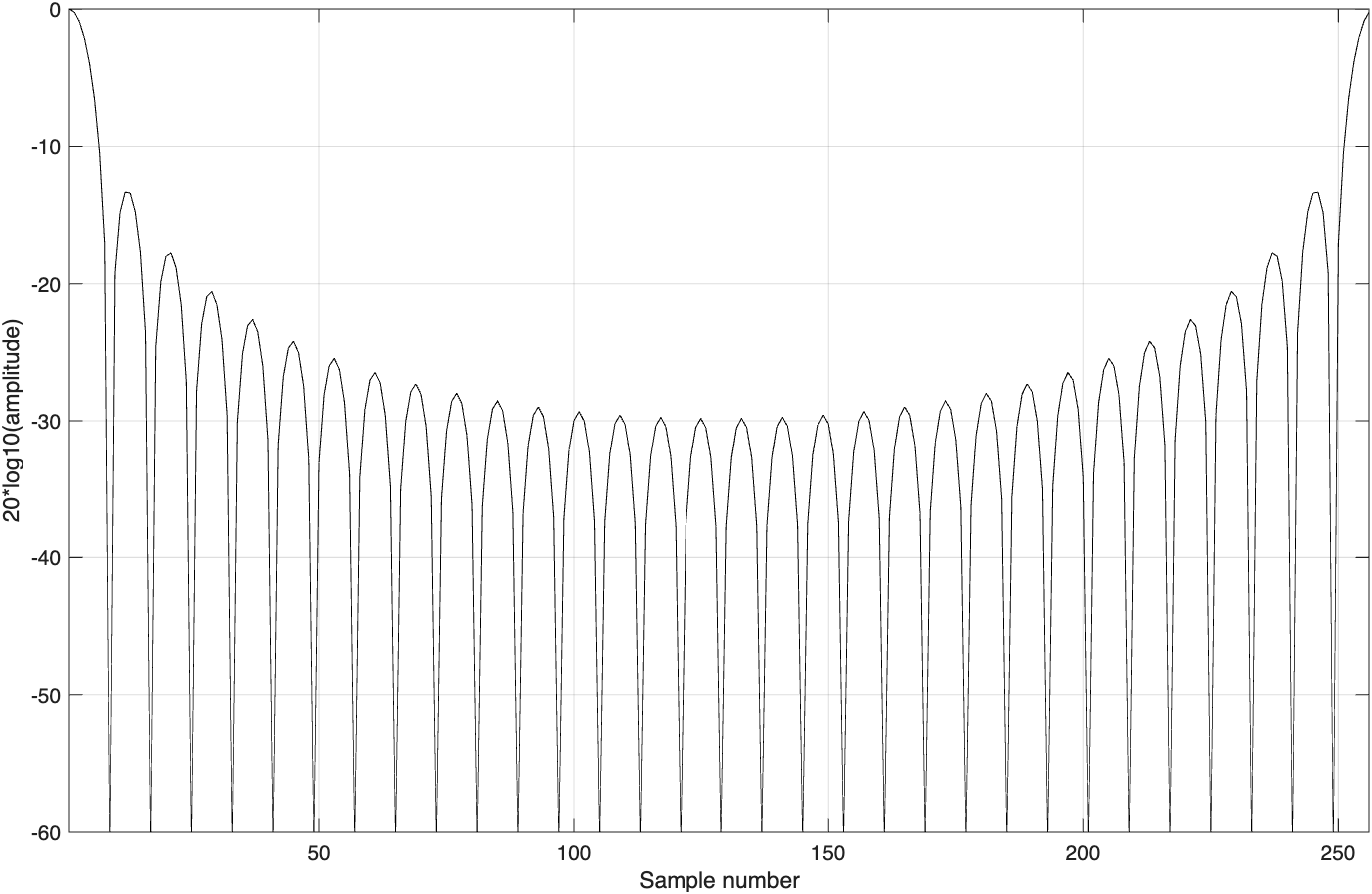
如果对所有的n都有f(n)=1，这就是熟知的矩形窗。这会导致吉布斯（Gibbs）现象，它显示为不连续点前后的过冲和波纹。图3.10所示为矩形窗的幅度谱。注意，第一副瓣比主瓣约低-13.46dB。在边缘附近的采样上加小量权的窗，在不连续点处将具有较小的过冲（较小的副瓣）。因此，与矩形窗相比，这是人们更期望的。不过，副瓣减少会被主瓣展宽所抵消，因此，恰当地选择窗序列是在副瓣减小和主瓣展宽之间不断地进行折中。表3.1和表3.2概括了一些常用窗对主瓣加宽与峰值降低的相应影响。

窗	零值到零值的波束宽度（以矩形窗做参考）	峰值衰减
矩形	1	1
汉明（Hamming）	2	0.73
汉宁（Hanning）	2	0.664
布莱克曼（Blackman）	6	0.577
凯撒（Kaiser）（\beta=6）凯撒（\beta=3）	2.76 1.75	0.683 0.882

窗	表达式	第一副瓣	主瓣宽度
矩形	w(n)=1	-13.46dB	1
汉明	w(n)=0.54-0.46\cos{(\frac{2\pi n}{N-1})}	-41dB	2
汉宁	w(n)=0.5[1-\cos{(\frac{2\pi n}{N-1})}]	-32dB	2
凯撒	w(n)=\frac{I_0[\beta\sqrt{1-(2n/N)^2}]}{I_0(\beta)} I_0是第一类零阶改进贝塞尔函数	\beta=2\pi时为-46dB	\beta=2\pi时为\sqrt{5}

方程（3.186）所定义的乘法过程等效于频域上的循环卷积。由此可见，X_w(k)是X(k)的损坏形式（或变形形式）。为了减小这种变形，我们将寻找一种具有窄主瓣和小副瓣的窗函数。另外，使用非矩形窗将把功率减小为1/P_w，式中

P_w=\frac{1}{N}\sum^{N-1}_{n=0}w^2(n)=\sum^{N-1}_{k=0}|W(k)|^2

由此得出，x_w(n)的离散功率谱（DPS）为

P_0^w=\frac{1}{P_wN^2}|X(0)|^2

P^w_k=\frac{1}{P_wN^2}\{|X(k)|^2+|X(N-k)|^2\};k=1,2,...,\frac{N}{2}-1

P^w_{N/2}=\frac{1}{P_wN^2}|X(N/2)|^2

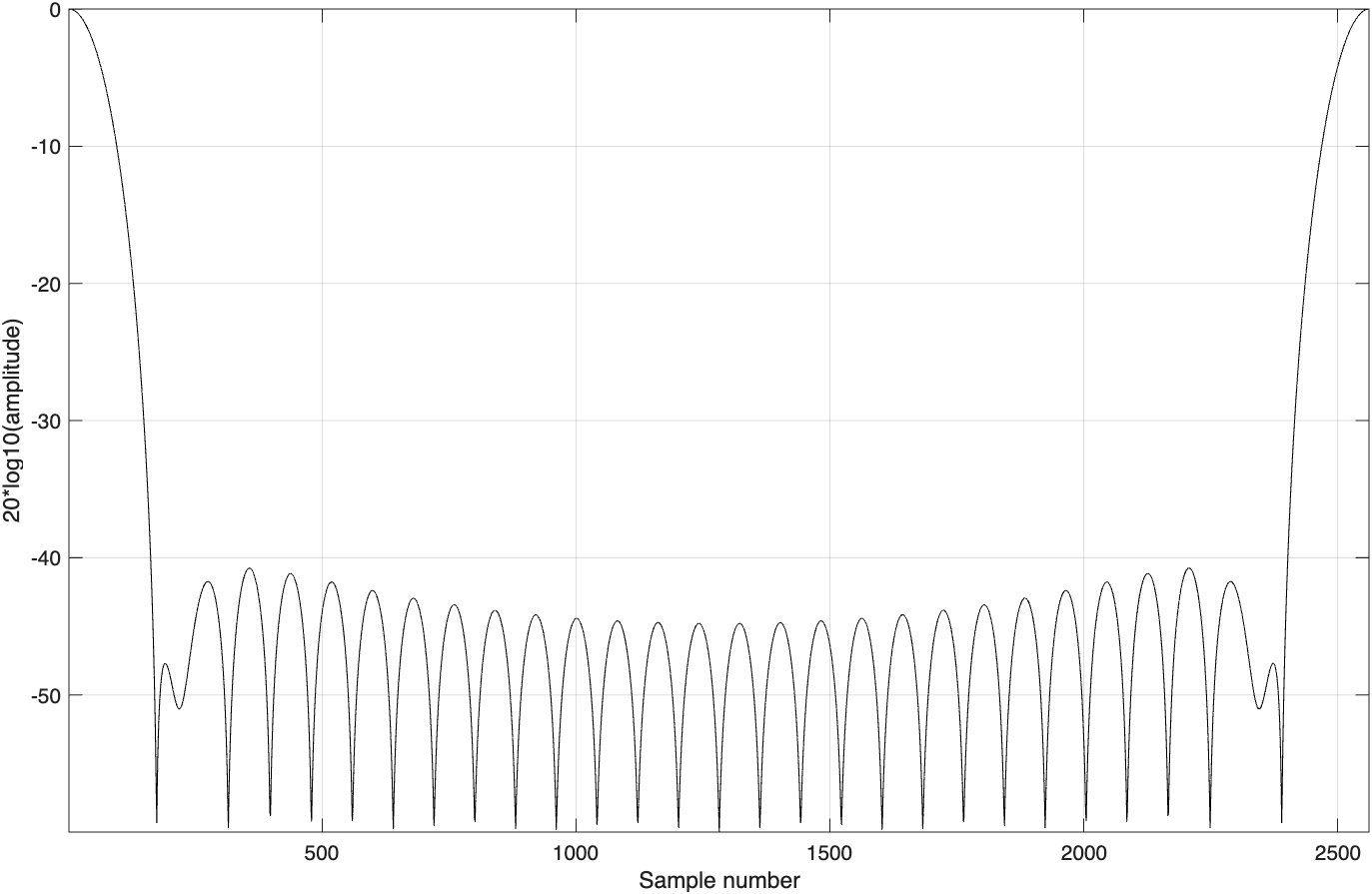
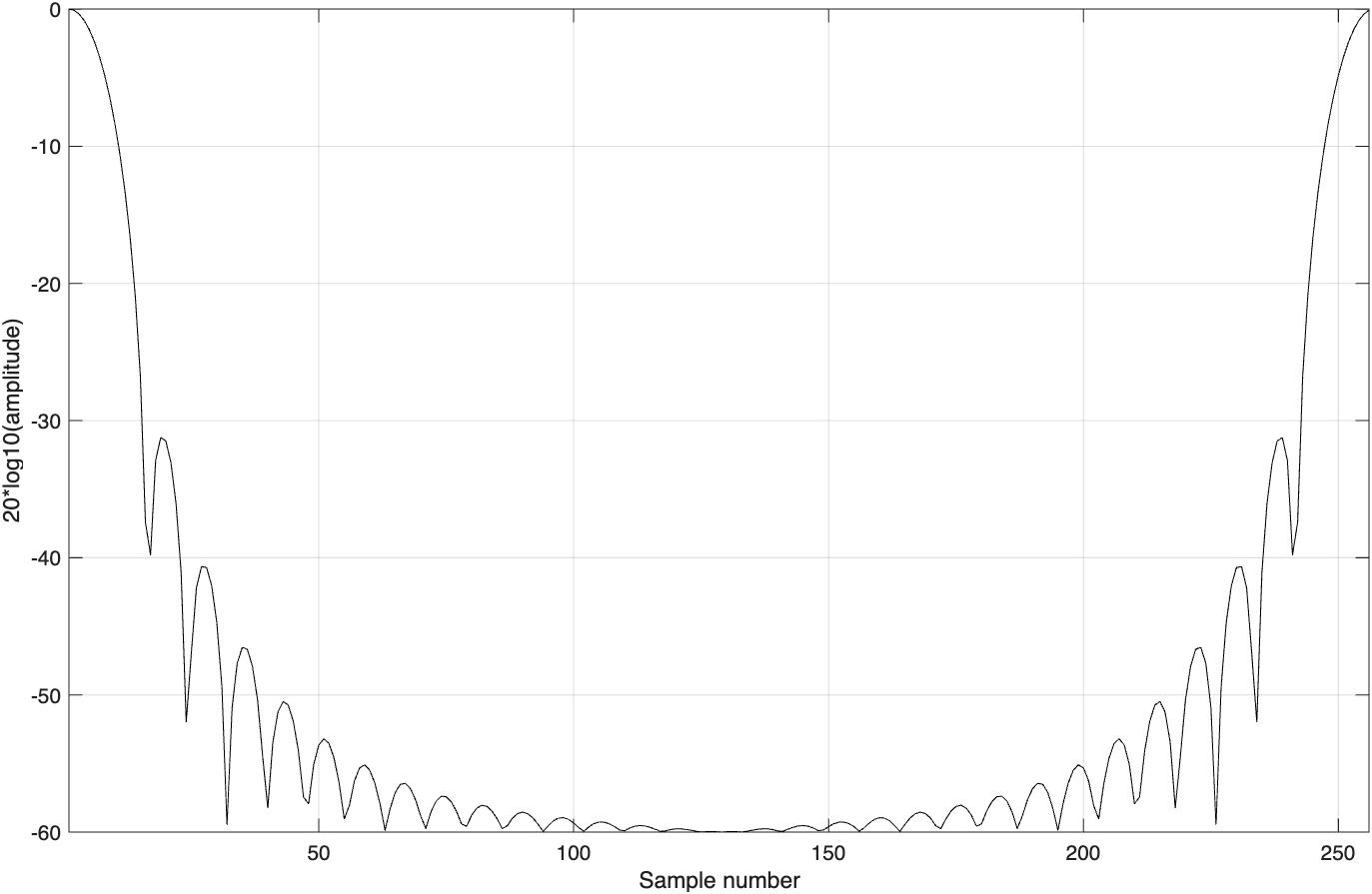
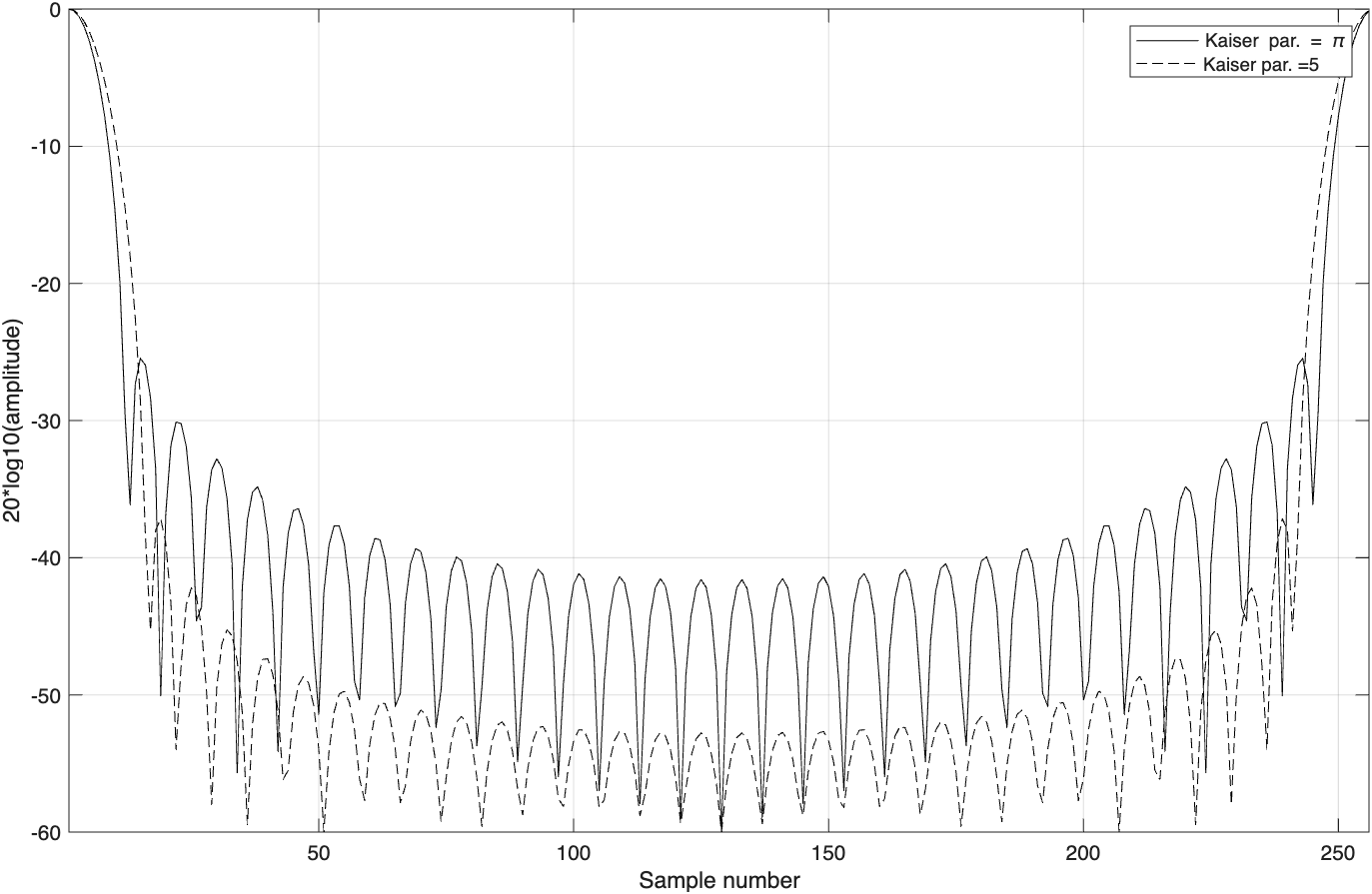
式中，由方程（3.188）确定。表3.2列出了一些常用窗的数学表达式。图3.11～图3.13给出了这些窗的频域特性。

四、匹配滤波器雷达接收机

五、模糊函数——模拟波形

MATLAB函数“single_pulse_ambg.m”

function [x] = single_pulse_ambg (taup)
% Computes the ambiguity of a single pulse
% 
% Inputs
    % taup      == pulsewidth in seconds
%Output
    % x         == ambiguity surface array
%
eps = 0.000001;
i = 0;
del = 2*taup/150;
for tau = -taup:del:taup
   i = i + 1;
   j = 0;
   fd = linspace(-5/taup,5/taup,151);
   val1 = 1. - abs(tau) / taup;
   val2 = pi * taup .* (1.0 - abs(tau) / taup) .* fd;
   x(:,i) = abs( val1 .* sin(val2+eps)./(val2+eps));
end

函数“single_pulse_ambg.m”实现方程（5.13）。语法如下：

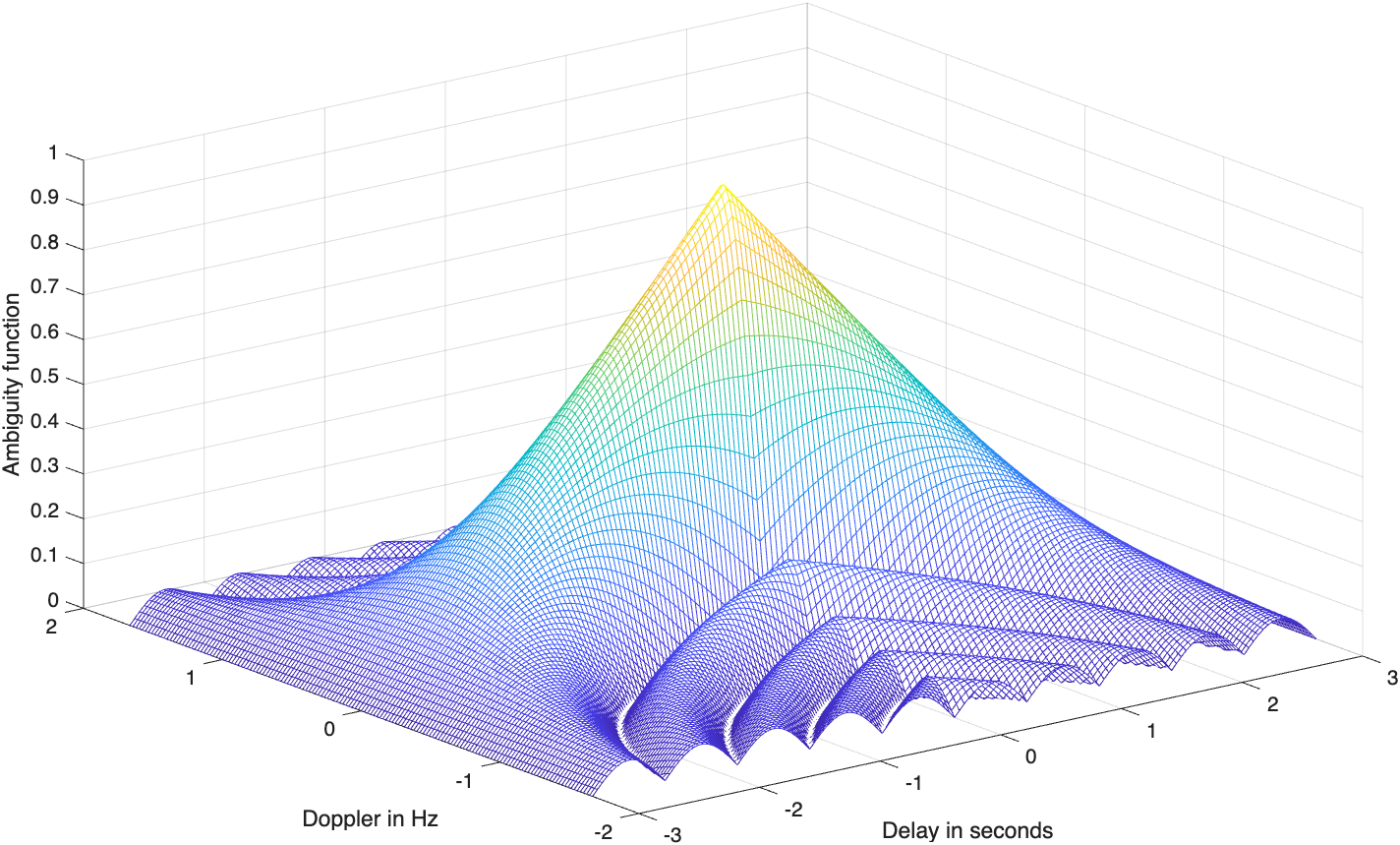
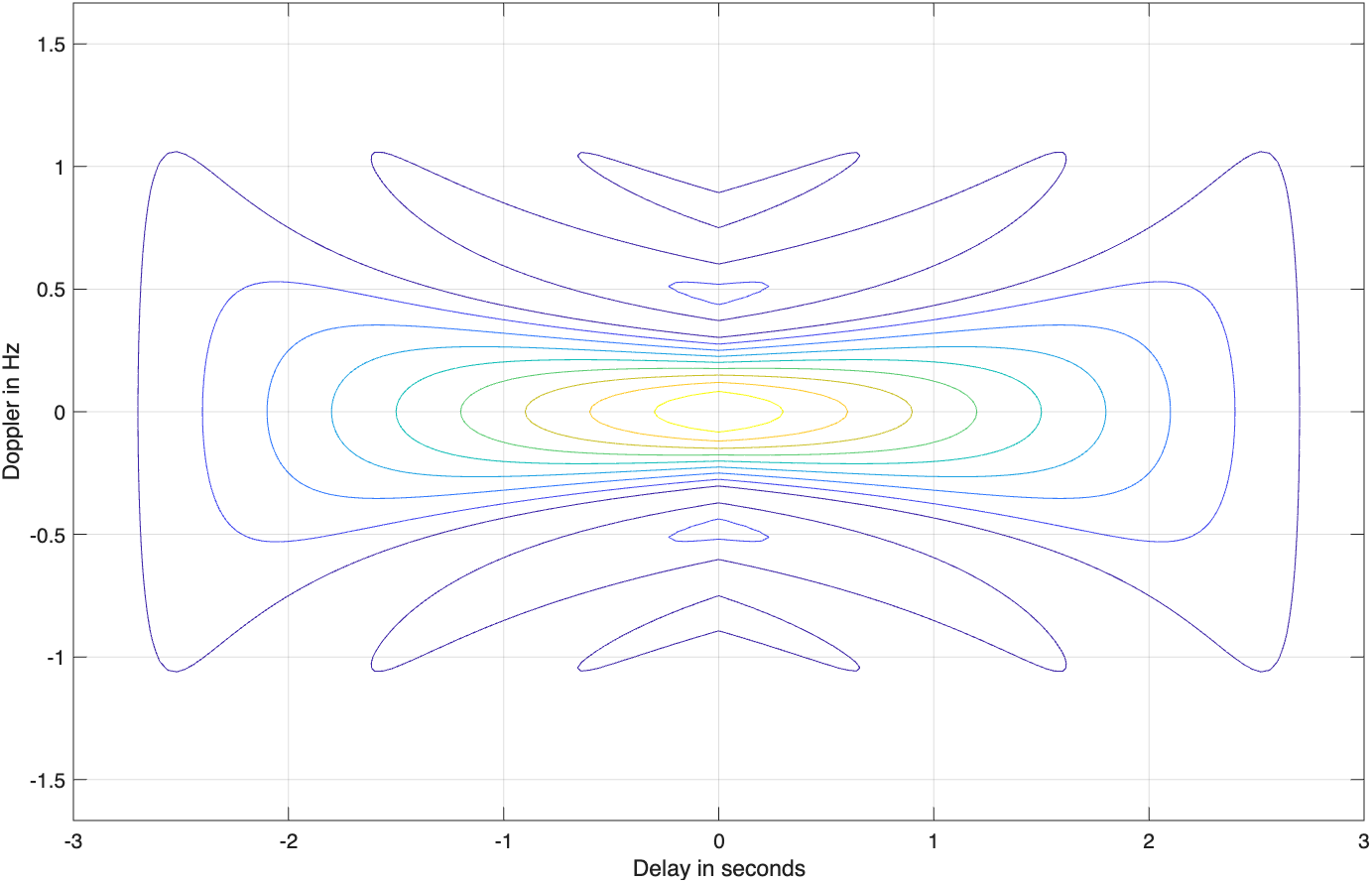
single_pulse_ambg[taup]

其中taup是脉冲宽度。图5.2（a）和图5.2（b）给出了单脉冲模糊函数的三维图与等值线图。设f_d=0，可得到沿时延轴\tau的模糊函数截线。更精确地说，

|\chi(\tau;0)|=(1-\frac{|\tau|}{\tau_0})^2\text{ }|\tau|\le\tau_0

注意，信号\tilde{x}(t)的时间自相关函数等于\chi(\tau;0)。类似地，沿多普勒轴的截线为

|\chi(0;f_d)|^2=|\frac{\sin{\pi\tau_0f_d}}{\pi\tau_0f_d}|^2

图5.3和图5.4分别给出了由方程（5.14）和方程（5.15）所定义的不确定性函数截线的图形。由于沿时延轴的零多普勒截线的范围在-\tau_0和\tau_0之间，那么，如果邻近目标至少相距秒，则它们就是不模糊的。

沿多普勒频率轴的零时延截线具有(\sin{x}/x)^2的形状。它从-\infty延伸至\infty。第一个零点出现在f_d=\pm1/\tau_0处。因此，可以不模糊地探测到频移间距为1/\tau_0的两个目标。我们可得出结论，单个脉冲的距离和多普勒分辨率受脉冲宽度\tau_0的限制。精细的距离分辨率要求采用一个很短的脉冲。遗憾的是，采用很短的脉冲需要很大的工作带宽，这可能将雷达平均发射功率限制为不实际的值。

MATLAB函数“lfm_ambg.m”

function x = lfm_ambg(taup, b, up_down)
% Implements Eq. (5.21) of textbook
%
% Inputs
    % taup      == pulsewidth in seconds
    % b         == bandwidth in Hz 
    % up_down	== 1 to indicate an up-chirp LFM
    % up_down   == -1 to indicate an down-chirp LFM
%
% Output
    % x         == ambiguity matrix
%
eps = 0.000001;
i = 0;
mu = up_down * b / taup;
del = 2*taup/200;
for tau = -1.*taup:del:taup
   i = i + 1;
   j = 0;
   fd = linspace(-1.5*b,1.5*b,201);
   val1 = 1. - abs(tau) / taup;
   val2 = pi * taup * (1.0 - abs(tau) / taup);
   val3 = (fd + mu * tau);
   val = val2 * val3;
   x(:,i) = abs( val1 .* (sin(val+eps)./(val+eps))).^2;
   end
end

函数“lfm_ambg.m”实现方程（5.21）。语法如下：

lfm_ambg[taup,b,up_down]

其中：

符号	说明	单位	状态
taup	脉冲宽度	s	输入
b	带宽	Hz	输入
up_down	升频线性调频脉冲up_down=1 降频线性调频脉冲up_down=-1	无	输入

符号

说明

单位

状态

taup

脉冲宽度

输入

带宽

输入

up_down

升频线性调频脉冲up_down=1

降频线性调频脉冲up_down=-1

无

输入

注意，沿多普勒频率轴的LFM模糊函数的截线与单个脉冲的截线相同。不必对此感到惊奇，因为脉冲形状没有改变（我们仅增加了频率调制）。但是，沿时延轴的截线变化很大。与未调制的脉冲截线相比，它现在要窄得多。在这种情况下，第一个零值发生在

\tau_{n1}\approx1/B

图5.6给出了对应方程（5.23）的不确定性函数中一条截线的图形。

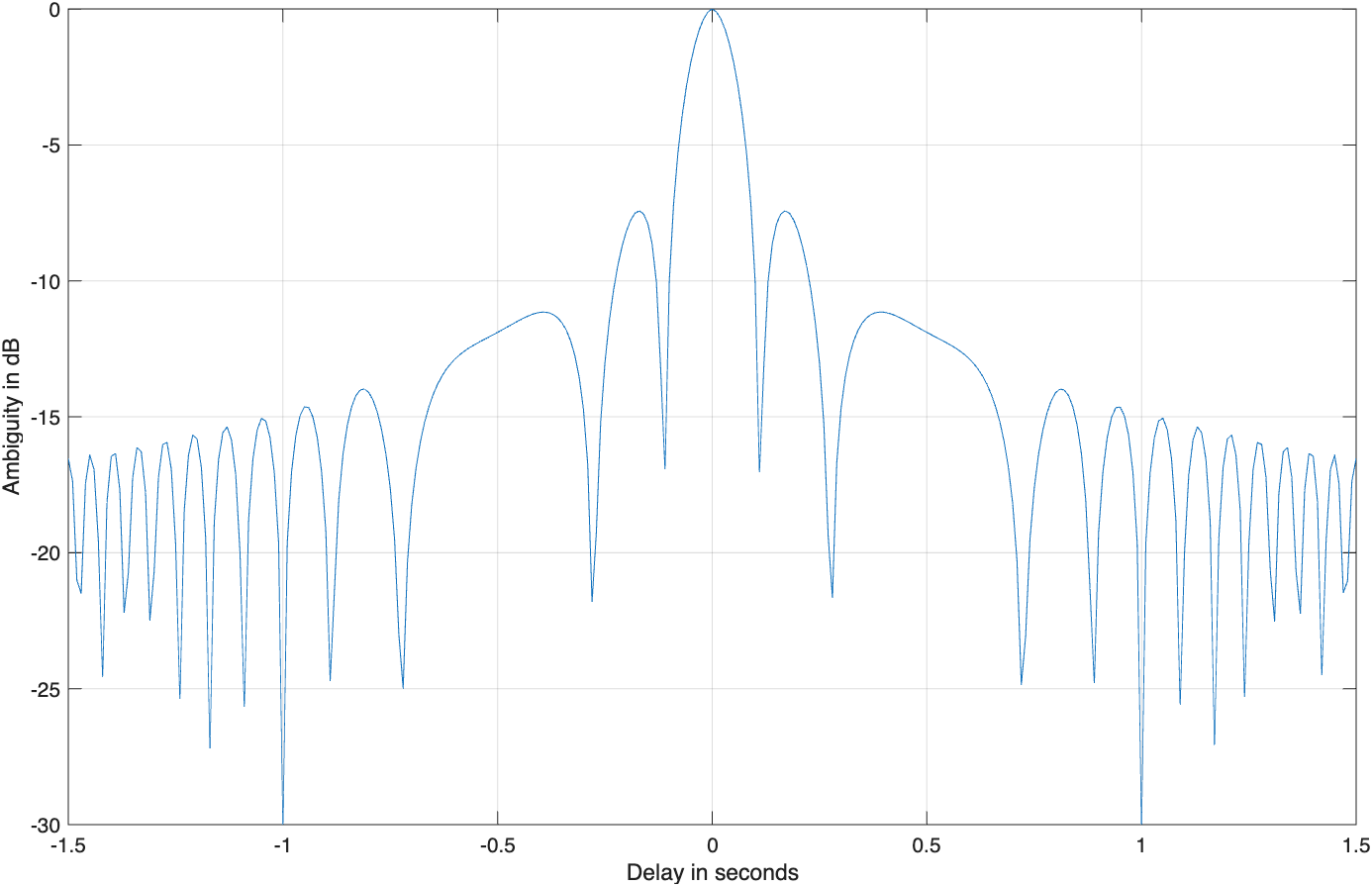
方程（5.24）表明匹配滤波器输出的有效脉冲宽度（压缩的脉冲宽度）完全由雷达带宽决定。由此沿时延轴的LFM模糊函数截线比未调制脉冲的截线要窄，其比例因子为

\xi=\frac{\tau_0}{(1/B)}=\tau_0B

\xi称为压缩比（也称为时间——带宽积和压缩增益）。所有这三个名称均可互换使用，意思相同。如方程（5.25）所示，压缩比也随着雷达带宽的增加而提高。

例：

用下列指标计算对应于LFM波形脉冲压缩之前和之后的距离分辨率：带宽B=1GHz，脉冲宽度\tau_0=10ms。

解：脉冲压缩之前的距离分辨率为

\Delta R_{uncomp}=\frac{c\tau_0}{2}=\frac{3\times10^8\times10\times10^{-3}}{2}=1.5\times10^5m

利用方程（5.24）得

\tau_{n1}=\frac{1}{1\times10^9}=1ns

\Delta R_{comp}=\frac{c\tau_{n1}}{2}=\frac{3\times10^8\times1\times10^{-9}}{2}=15cm

MATLAB函数“train_ambg.m”

function x = train_ambg(taup, n, pri)
% This function implements Eq. (5.37) of textbook
% 
% Inputs
    % taup      == pulse width in seconds
    % n         == number of pulses in train
    % pri       == pulse repetition interval in seconds
%
% Outputs
    % x         == ambiguity matrix
%
if (taup >= pri/2)
	'ERROR. Pulse width must be less than the PRI/2.'
	return
end
eps = 1.0e-6;
bw = 1/taup;
q = -(n-1):1:n-1;
offset = 0:0.031:pri;
[Q, S] = meshgrid(q, offset);
Q = reshape(Q, 1, length(q)*length(offset));
S = reshape(S, 1, length(q)*length(offset));
tau = (-taup * ones(1,length(S))) + S    ;
fd = -bw:0.011:bw;
[T, F] = meshgrid(tau, fd);
Q = repmat(Q, length(fd), 1);
S = repmat(S, length(fd), 1);
N = n * ones(size(T));
val1 = 1.0-(abs(T))/taup;
val2 = pi*taup*F.*val1;
val3 = abs(val1.*sin(val2+eps)./(val2+eps));
val4 = abs(sin(pi*F.*(N-abs(Q))*pri+eps)./sin(pi*F*pri+eps));
x = val3.*val4./N;
[rows, cols] = size(x);
x = reshape(x, 1, rows*cols);
T = reshape(T, 1, rows*cols);
indx = find(abs(T) > taup);
x(indx) = 0.0;
x = reshape(x, rows, cols);
return

函数“train_ambg.m”实现方程（5.37）。语法如下：

train_ambg[taup,n,prt]

其中：

符号	说明	单位	状态
taup	脉冲宽度	s	输入
n	串中的脉冲个数	无	输入
pri	脉冲重复间隔	s	输入

图5.8（a）和图5.8（b）给出了N=5、\tau_0=0.4、T=1时的三维模糊图及相应的等值线图。图5.8（c）和图5.8（d）分别给出了模糊函数中零多普勒和零时延截线图。沿频率轴的模糊函数峰值位于频率f=1/T的整数倍处。沿时延轴的模糊函数峰值的宽度为2\tau_0。沿多普勒轴的峰值宽度为1/(N-1)T。

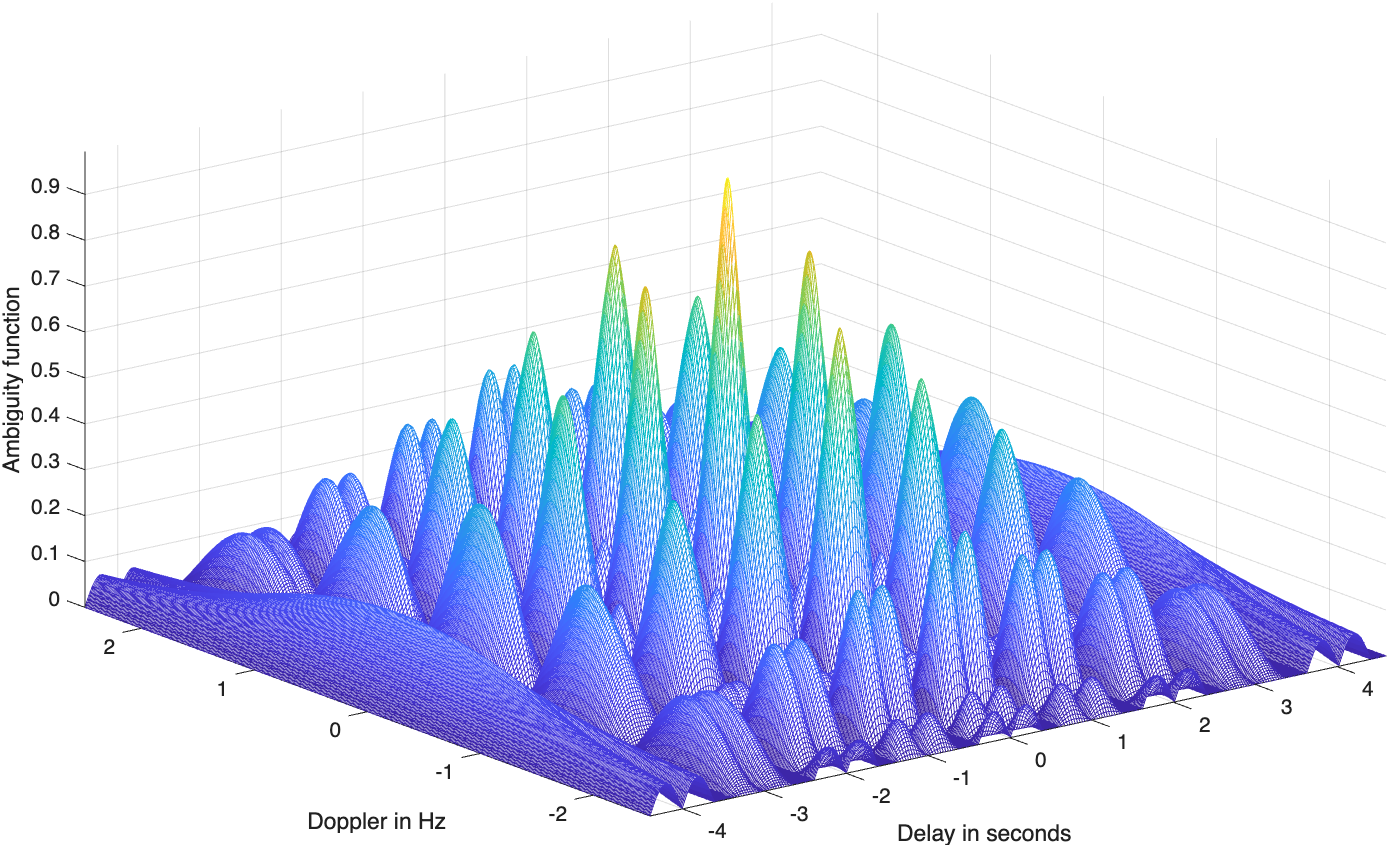
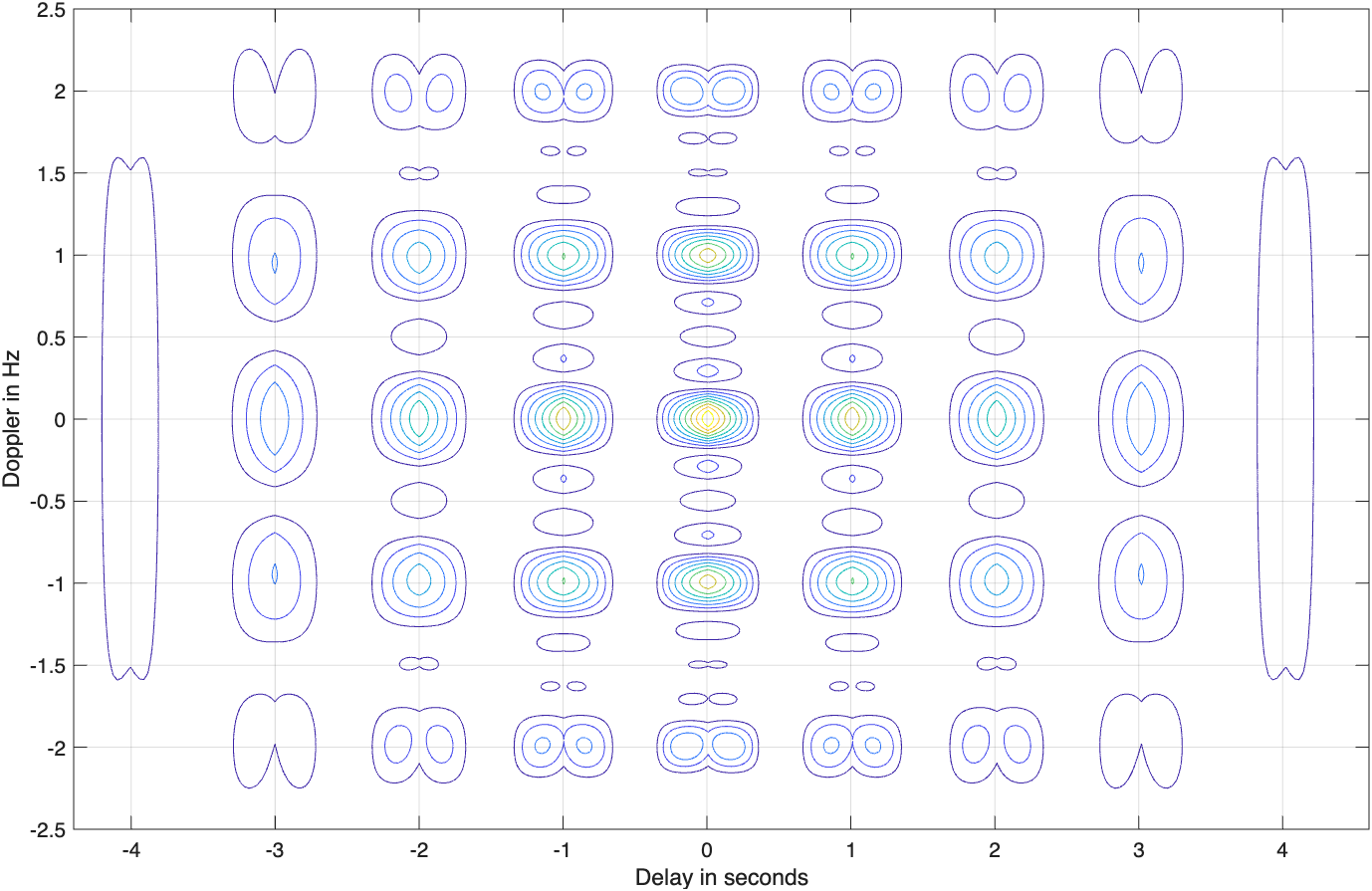
MATLAB函数“train_ambg_lfm.m”

function x = train_ambg_lfm(taup, n, pri, bw)
% This function implemenst Eq. (5.43) of textbook
%
% Inputs
    % taup      == pulsewidth in seconds
    % n         == number of pulses in train
    % pri       == pulse repetition interval in seconds
    % bw        == the LFM bandwidth in Hz
%
%Outputs
    % x         == array of bimodality function	
%
if (taup >= pri/2)
	'ERROR. Pulse width must be less than the PRI/2.'
	return
end
	
eps = 1.0e-6;

q = -(n-1):1:n-1;
offset = 0:0.033:pri;
[Q, S] = meshgrid(q, offset);
Q = reshape(Q, 1, length(q)*length(offset));
S = reshape(S, 1, length(q)*length(offset));

tau = (-taup * ones(1,length(S))) + S ;
fd = -bw:0.033:bw;
[T, F] = meshgrid(tau, fd);

Q = repmat(Q, length(fd), 1);
S = repmat(S, length(fd), 1);
N = n * ones(size(T));

val1 = 1.0-(abs(T))/taup;
val2 = pi*taup*(F+T*(bw/taup)).*val1;
val3 = abs(val1.*sin(val2+eps)./(val2+eps));
val4 = abs(sin(pi*F.*(N-abs(Q))*pri+eps)./sin(pi*F*pri+eps));
x = val3.*val4./N;

[rows, cols] = size(x);
x = reshape(x, 1, rows*cols);
T = reshape(T, 1, rows*cols);
indx = find(abs(T) > taup);
x(indx) = 0.0;
x = reshape(x, rows, cols);

return

函数“train_ambg_lfm.m”实现方程（5.43）。语法如下：

x=train_ambg_lfm(tap,n,pri,bw)

其中：

符号	说明	单位	状态
taup	脉冲宽度	s	输入
n	串中的脉冲个数	无	输入
pri	脉冲重复间隔	s	输入
bw	LFM带宽	Hz	输入
x	双峰函数阵列	无	输出

注意，当设“bw”的值为0时，这个函数产生与函数“train_ambg.m”相同的结果。在这种情况下，方程（4.43）与方程（4.35）是一样的。图5.10（a）和图5.10（b）给出了除增加LFM调制及N=3的脉冲以外，其他与前一节中列出势力相同的情况下，其模糊函数图及相应的等值线图。

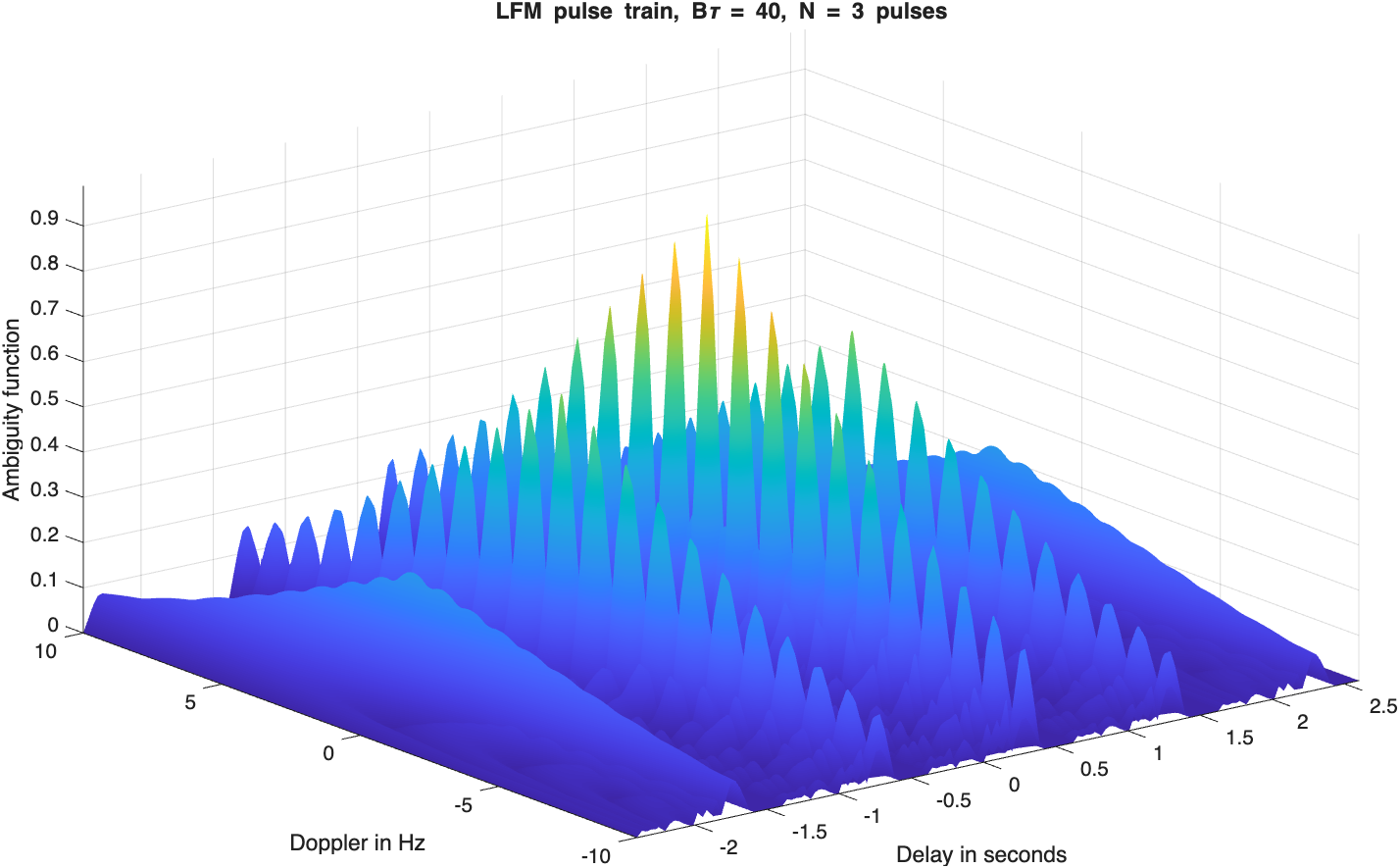
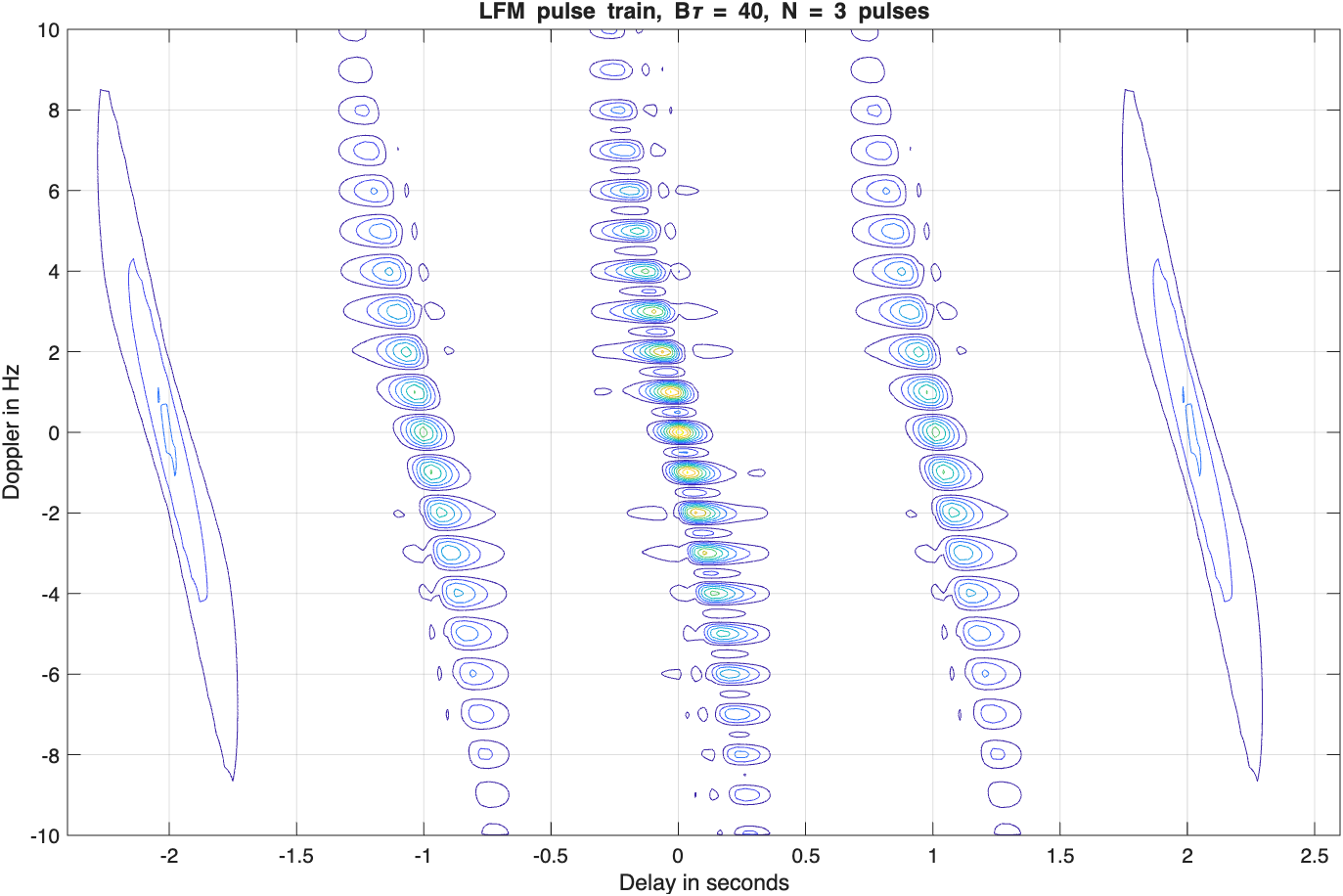
六、模糊函数——离散编码波形

脉冲串编码

这类编码背后的想法是将长度为T_p的较长脉冲分割成N个子脉冲，每个子脉冲是脉宽为\tau_0且幅度为1或0的矩形脉冲。因此编码U是1和0的序列。更精确地说，表示这类编码的信号可写为

x(t)=e^{j\omega_0t}\sum^N_{n=1}P_n(t)=e^{j\omega_0t}\sum^N_{n=1}a_nRect(\frac{t}{\tau_0})

一种生成脉冲串类编码的方法是设置

a_n=\begin{cases} 1 &n-1=0 &\text{模}q \\0 &n-1\ne0 &\text{模}q \end{cases}

其中q是一个正整数，它将N-1均匀分成q份。也即

M-1=(N-1)/q

其中M 是编码中1的个数。例如，当N=21且q=5，那么M=5，因此最终编码为

\{U\}=\{ 10000 \text{ }10000 \text{ }10000\text{ }10000\text{ }1\}

这在图6.1中进行了说明。在前面的章节中，这个编码是用下面的连续时域信号表示的，

x_1(t)=e^{j\omega_0t}\sum^4_{m=0}Rect{\frac{t-mT}{\tau_0}}

其中周期为T=5\tau_0。类似地，得

\frac{T_p}{M-1}\equiv T

且方程（6.10）现在可写为

x(t)=e^{j\omega_0t}\sum^{M-1}_{m=1}Rect(\frac{t-m(\frac{T_p}{M-1})}{\tau_0})

第5章中推导了相干脉冲串的模糊函数表达式。比较方程（6.16）和方程（5.27），除了一些常数外，当方程（6.15）中的条件为真时，这两个方程是等价的。因此方程（6.16）中定义的信号的模糊函数为

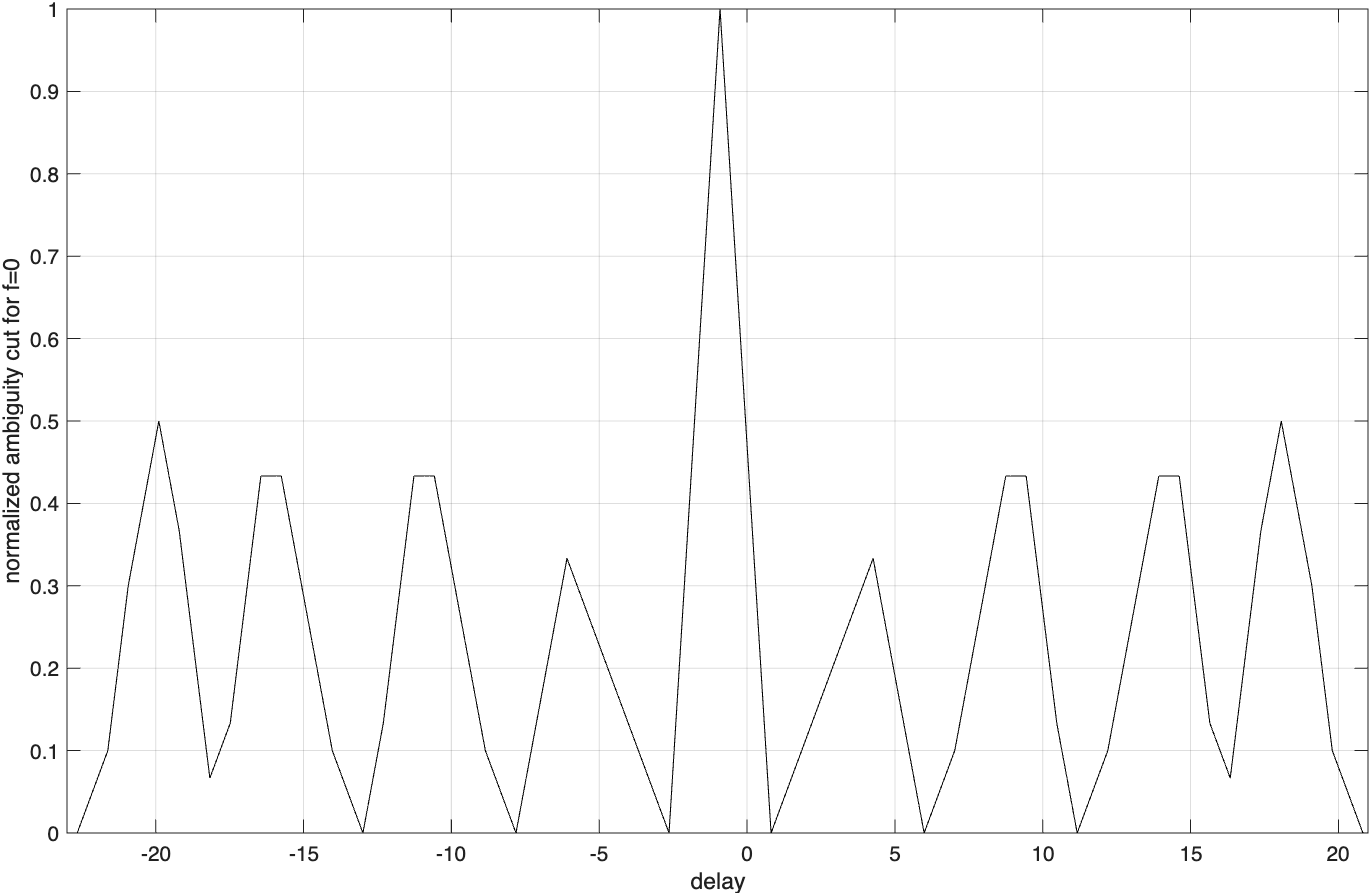
|\chi(\tau;f_d)|=\sum^{M}_{k=-M}|\frac{\sin{[\pi f_d([M-|k|]\frac{T_p}{M-1})]}}{\sin{(\pi f_d\frac{T_p}{M-1})}}| =|\frac{\sin{[\pi f_d(\tau_0-|\tau-\frac{kT_p}{M-1}|)]}}{\pi f_d}|

由方程（6.17）可推导出模糊函数的零多普勒和零时延截图，它们是

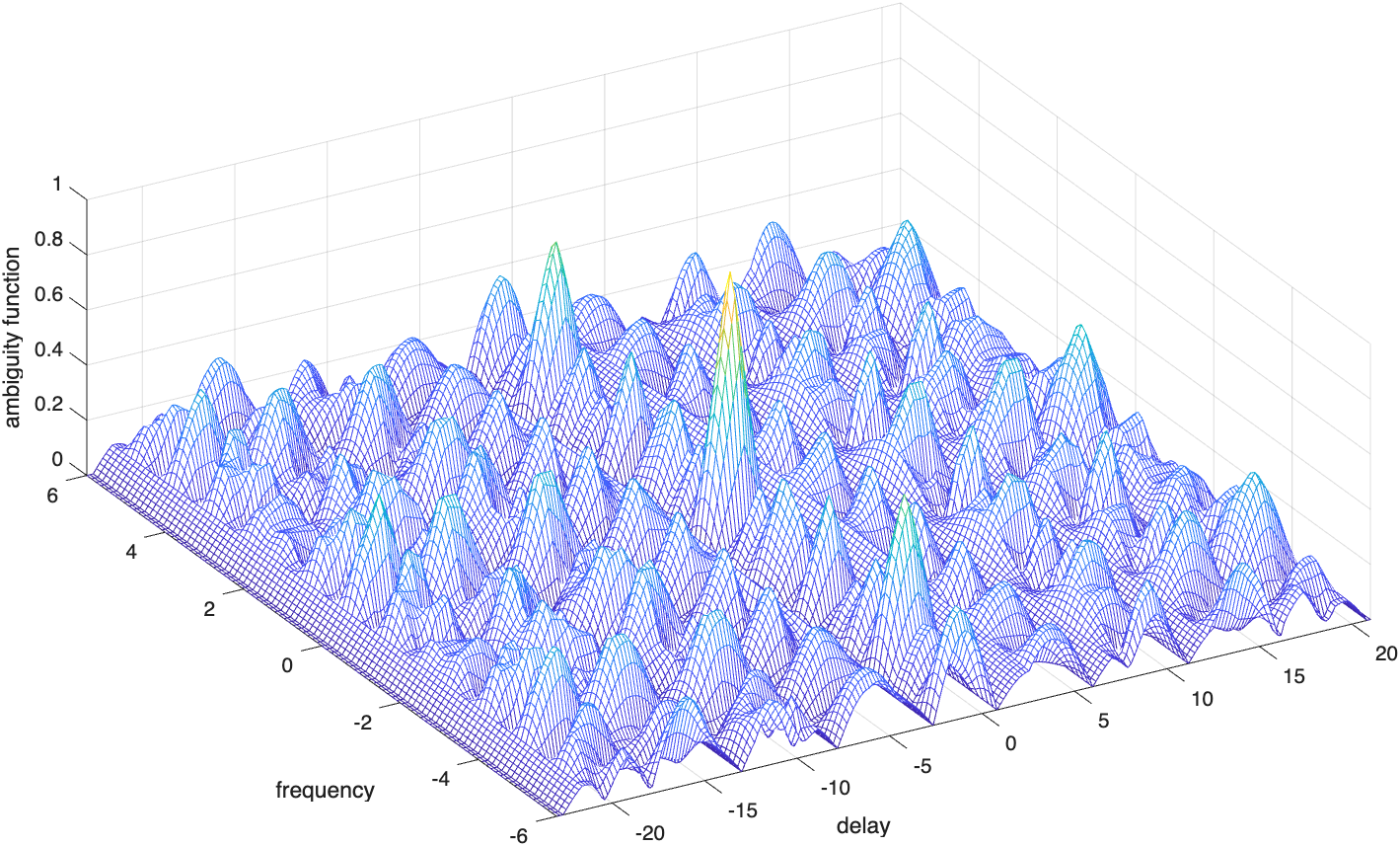
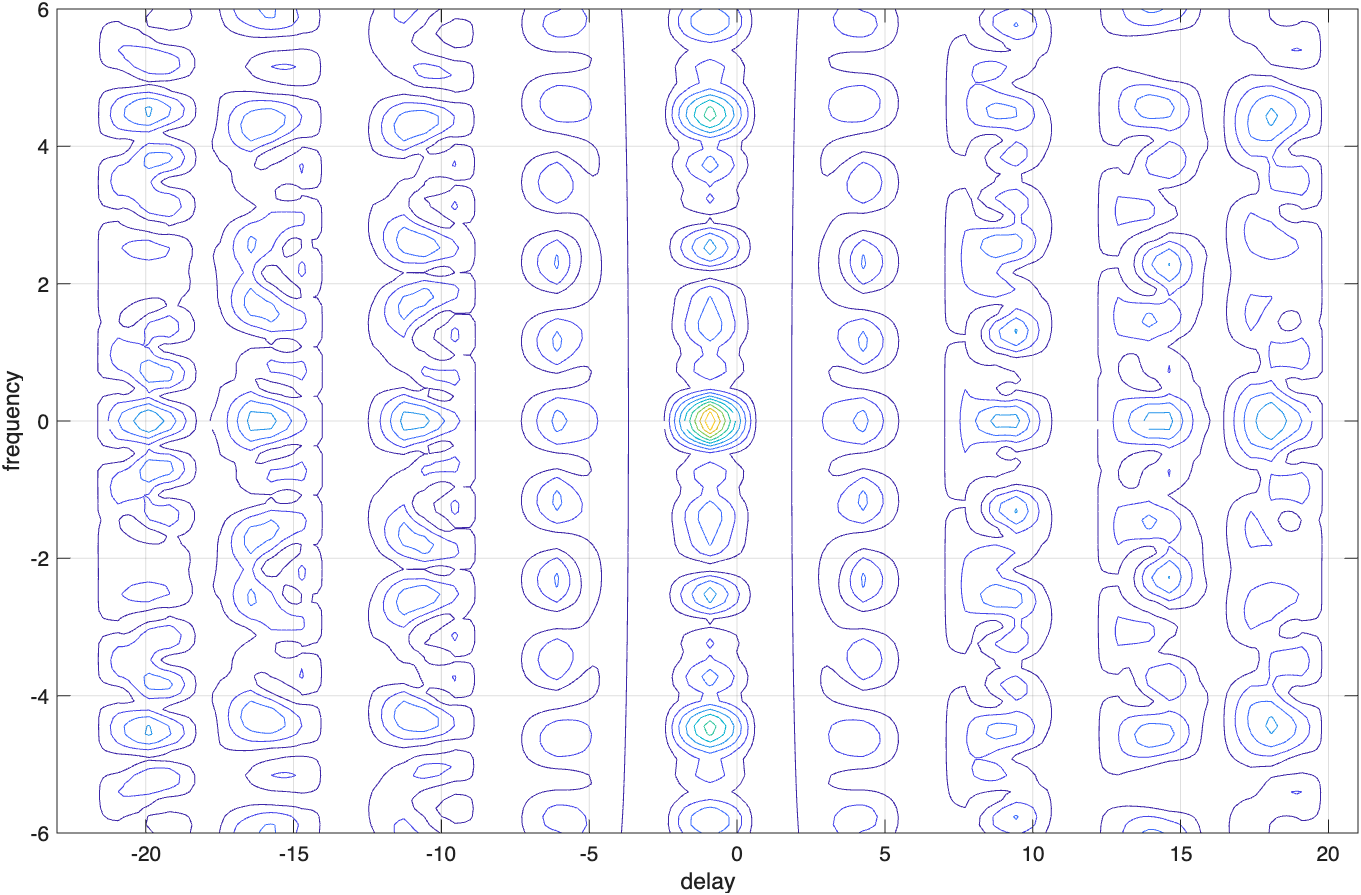
|\chi(\tau;0)|=M\tau_o\sum^{M}_{k=-M}[1-\frac{k}{M}](1-\frac{|\tau-\frac{kT_p}{M-1}|}{\tau_0})

|\chi(0;f_d)|=\sum^M_{k=-M}|\frac{\sin{[\pi Mf_d(\frac{T_p}{M-1})]}}{\sin{\pi f_d\frac{T_p}{M-1}}}||\frac{\sin{\pi f_d\tau_0}}{\pi f_d\tau_0}|

图6.2（a）描绘出了图6.1给出的编码的三维模糊图，而图6.2（b）给出了对应的等值线图。

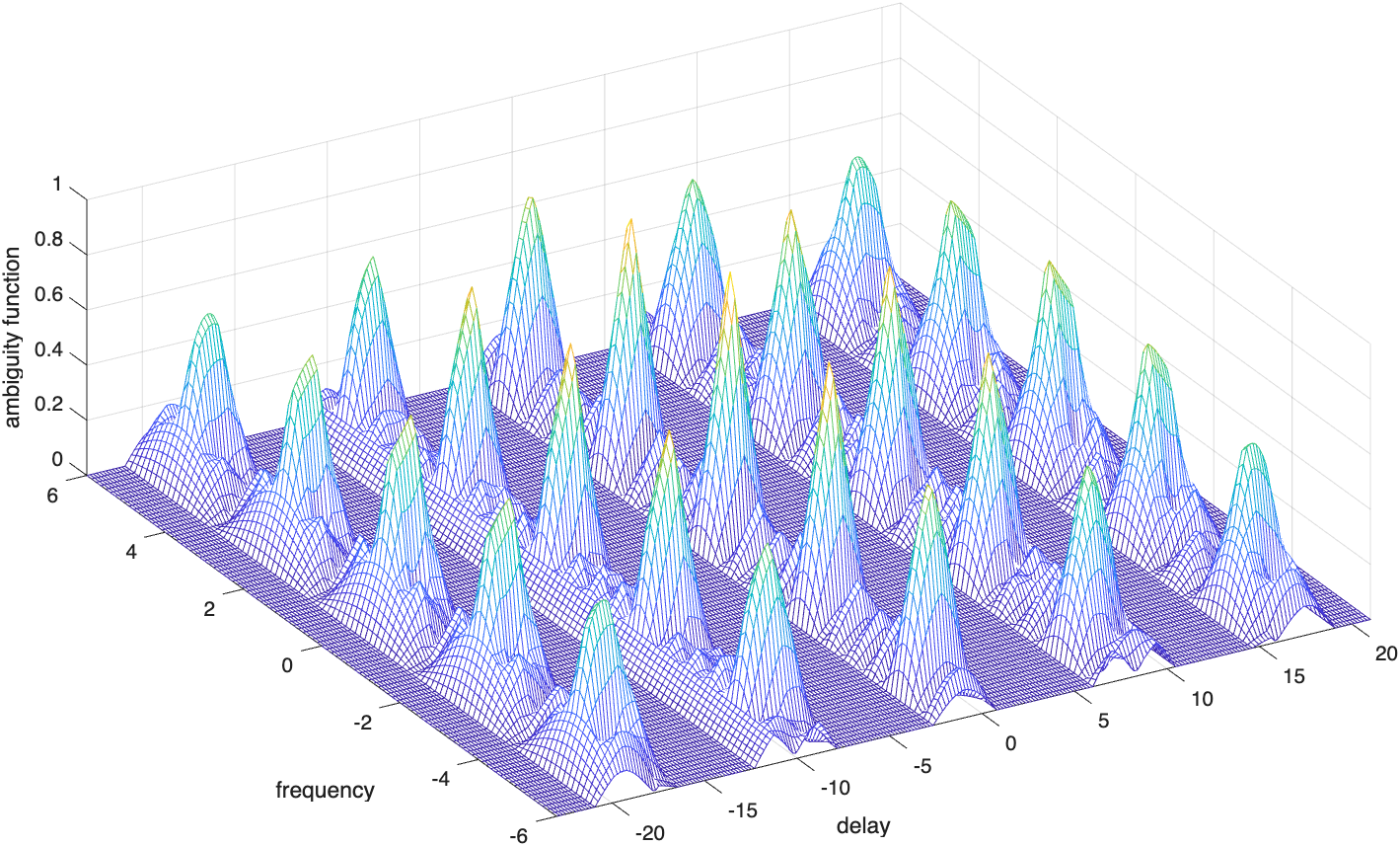
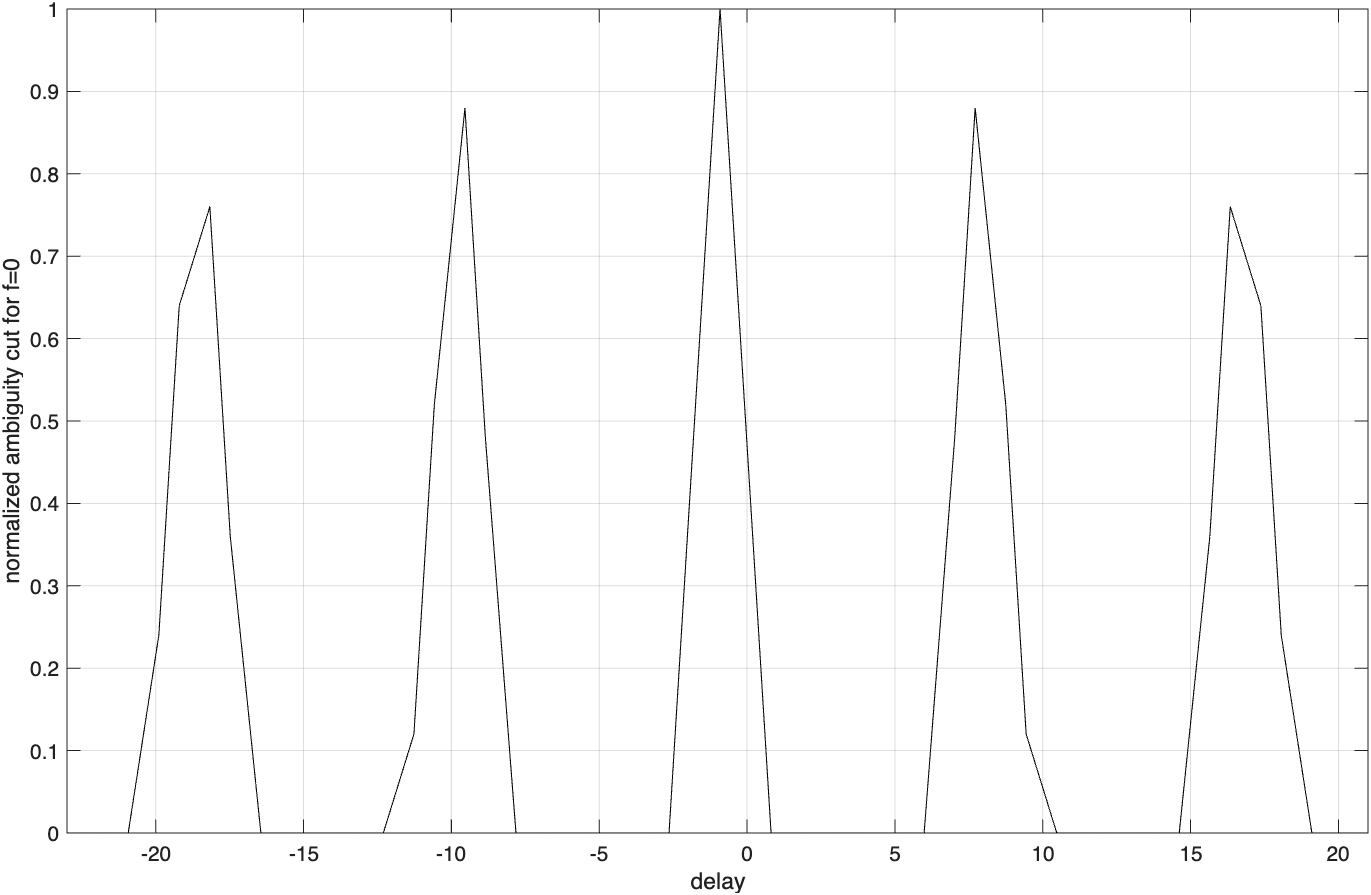
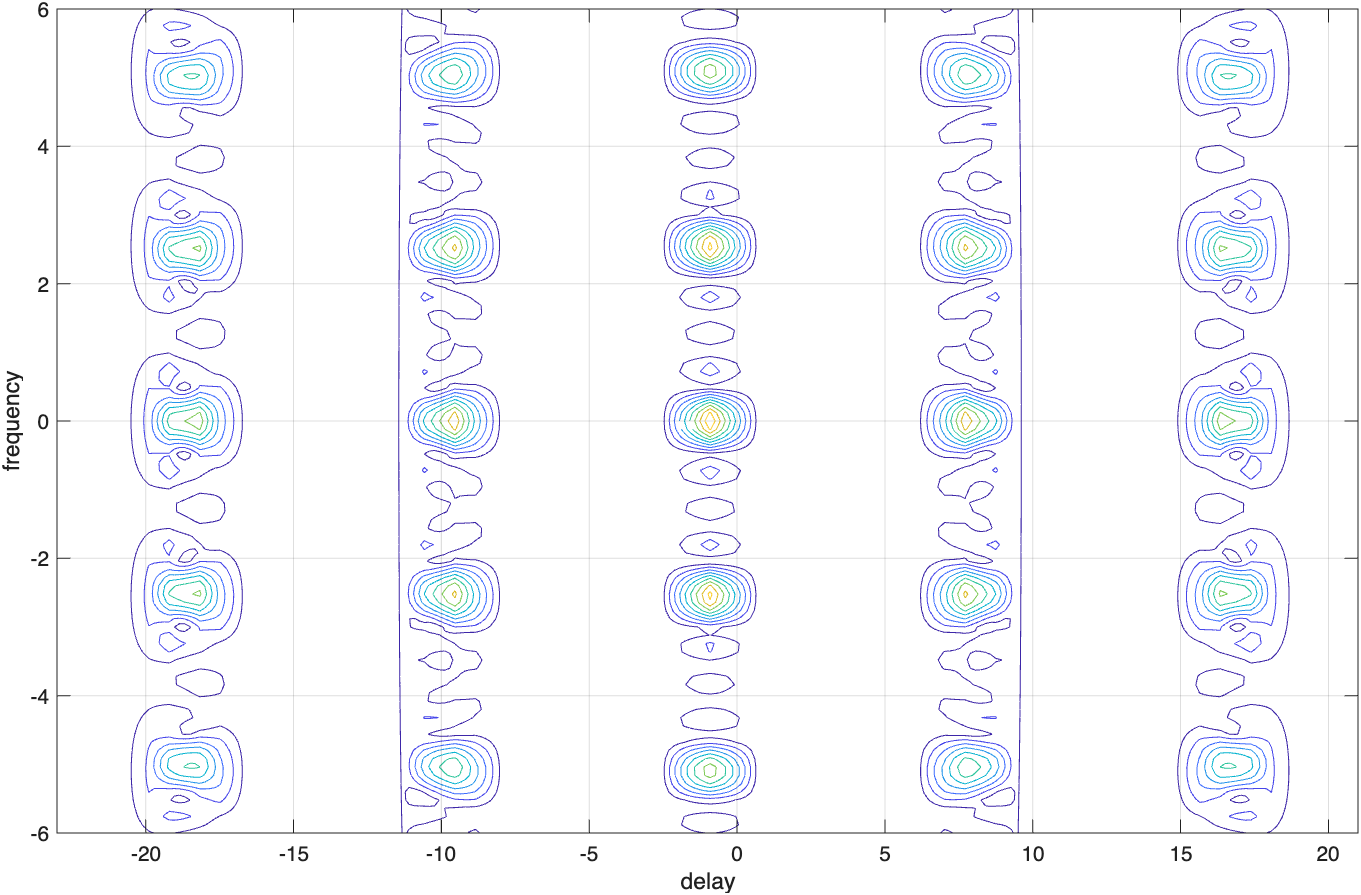
图6.2（c）给出了一个脉冲串编码模糊函数的等值线截图的草图。很显然，模糊函数主瓣宽度（即分辨率）与编码长度直接相关。正如我们预见的，编码越长，产生的主瓣越窄，因此分辨率比较短的编码更高。进一步观察图6.2表明，这个模糊函数有很强的栅瓣及很高的旁瓣电平。这些栅瓣和旁瓣是由编码内的1均匀等间隔分布（即编码的周期性）直接造成的。通过去除编码的周期结构，即以不均匀间隔放置脉冲，可以大大降低这些栅瓣和旁瓣，这称为编码参差（PRF参差）。

例如，考虑一个长度N=21的脉冲串编码。使用以下序列a_n，

\{a_n\}=1 \text{ }n=1,4,6,12,15,21

可得一个参差脉冲串编码。因此，得到的编码为

\{U\}=\{100101000001001000001\}

图6.3给出了对应于这个编码的模糊图。如图6.3所述，对应于一个参差脉冲串编码的模糊函数接近于图钉的形状。许多人已经对最优参差编码的选择做了广泛研究。Resnick定义最优参差脉冲串编码就是那些模糊函数具有绝对均匀且等于1旁瓣电平的脉冲串编码^1。其他研究者也引入了对最优参差的不同定义，除了考虑各个研究者分析的不同应用，各种定义各有优势。

1 Resnick,J.B.,High Resolution Waveforms Suitable for a Multiple Target Environment,MS thesis,MIT,Cambridge,MA,June 1962.

站内导航

常用MATLAB函数及示例